信息
Title: Autoregressive Pretraining with Mamba in Vision
Author: Sucheng Ren, Xianhang Li, Haoqin Tu, Feng Wang, Fangxun Shu, Lei Zhang, Jieru Mei, Linjie Yang, Peng Wang, Heng Wang, Alan Yuille, Cihang Xie
Year: 2024
Publish: arxiv
Code: https://github.com/OliverRensu/ARM
Keyword: Mamba, 自回归, 扫描策略
背景
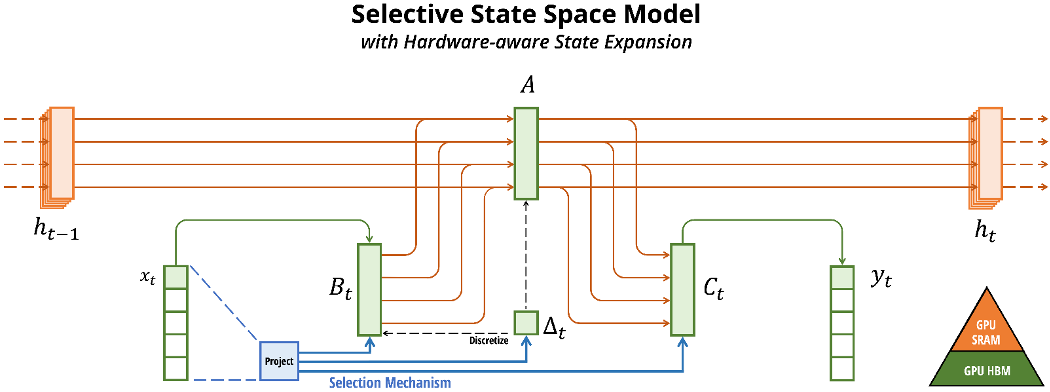
SSM在NLP和视觉领域由于可以用线性复杂度处理长序列关系,Mamba利用选择扫描机制进行了实现
经典SSM模型:
h′(t)y(t)=Ah(t)+Bx(t)=Ch(t)
零阶保持离散化:
A=exp(ΔA)B=(ΔA)−1(exp(ΔA)−I)⋅ΔB
定义快速计算:
Ky=(CB,CAB,…,CAkB,…)=x∗K
但之前主要集中于有监督学习(泛化性和scaling)
相较于其它方法,自回归
SSM:
没有Softmax的线性attention可以视为一种退化的SSM
S5在S4的基础上增添了多入多出SSM和并行扫描策略
RWKV是一种类似于像有两个SSM一样运行的RNN,融合了状态拓展和输入无关的门控机制
Mamba是使用了隐藏状态拓展的数据无关的SSM层
自回归:
Vision Mamba:
- Vim:Vim层使用了堆叠的纯Mamba层,使用了双向扫描
- Vmamba:使用了VSS层,结合了Mamba层和2D卷积,使用了与类似Swin的金字塔结构,每个VSS层通过2D深度卷积-CrossScan进行处理
- Mamba-ND:增强Mamba到多维度
- LocalMamba:对图像切分,然后对于这些window使用SSM
- EfficientMamba使用空洞采样来减少计算量
Mamba背景
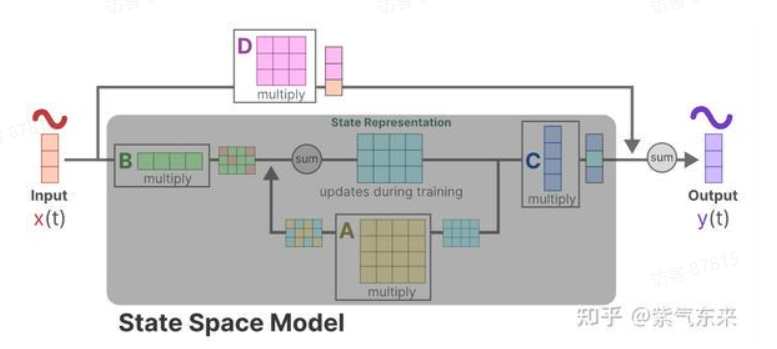
状态空间模型使用拓展的隐藏状态ht对将1D的序列进行建模,其中,隐藏状态通过参数A,B,C随着时间变化,变化符合线性常微分方程:
h′(t)y(t)=Ah(t)+Bx(t)=Ch(t)
引入一个时间缩放参数Δ,使用零阶保持来对连续的A,B进行离散化:
对第一个线性常微分方程两边同乘e−At可以得到:
e−Ath′(t)=e−AtAh(t)+e−AtBx(t)
移项化简:
dtd(e−Ath(t))=e−AtBx(t)
同时取积分:
e−Ath(t)−h(t0)=∫t0te−AτBx(τ)dτ
左乘eAt并移项得h(t):
h(t)=eAth(t0)+∫t0teA(t−τ)Bx(τ)dτ
进行离散化,代入k=(k+1)T:
h((k+1)T)=eA(k+1)Th(kT)+∫kT(k+1)TeA((k+1)T−τ)Bx(τ)dτ
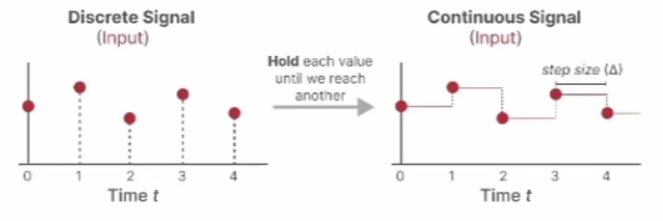
零阶保持的假设是:
x(t)=xk,t∈[kT,(k+1)T),
那么可以令α=kT+T−τ对上式进行化简:
h((k+1)T)=eATh(kT)+(∫0TeAαdα)Bx(kT)
A=exp(ΔA)B=(ΔA)−1(exp(ΔA)−I)⋅ΔB
最终变为:
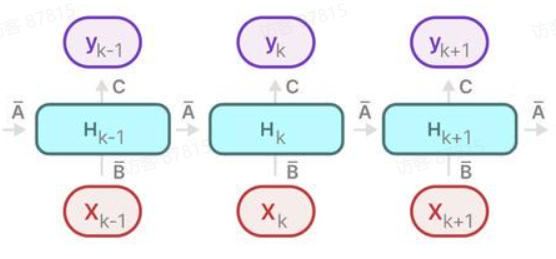
h′(t)yt=Aht−1+Bxt,=Cht.
ht=Aˉht−1+Bˉxt
ht−1=Aˉht−2+Bˉxt−1
ht=Aˉ2ht−2+AˉBˉxt−1+Bˉxt=k=0∑tAˉkBˉxt−k
yt=Cht=C(k=0∑tAˉkBˉxt−k)=k=0∑tCAˉkBˉxt−k
而离散卷积:
(x∗h)[t]=k=0∑N−1x[k]h[t−k]
定义一个矩阵K进行快速计算:
Ky=(CB,CAB,…,CAkB,…)=x∗K
其中,k∈[0,L),L为输入序列长度,K∈RL可以被视为卷积核,这可以使得Mamba像自回归一样对输入序列建模
贡献点(对于输入特征进行改进):
- 将自回归预训练与Mamba模型结合,探索视觉Mamba架构的自监督范式
- 利用聚类将临近的patch聚为簇作为输入,替代基于像素或patch的策略
- 对于将2D图像映射为1D输入,证明逐行扫描已经足够有效
方法
视觉中自监督
图像和文本信息存在本质上的差异,没有很强的因果关系:
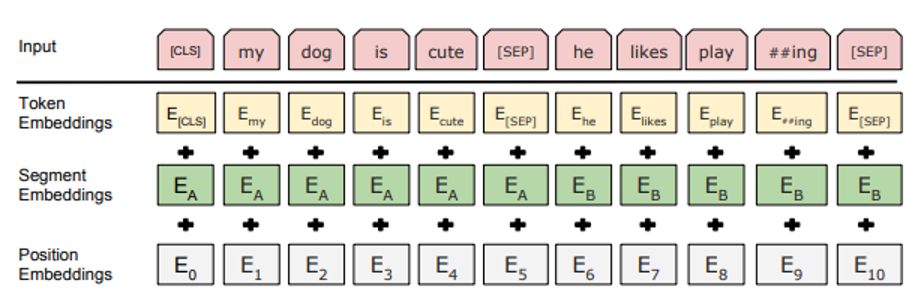
- 文本的自监督研究主要集中于自回归,可以做到scaling law
- 图像的自监督研究可以分为对比学习,MAE,自回归,位置预测,Jigsaw…,对于哪种方法更有效和如何scale模型还没有统一的结论,主要难点在于:
- 实现有效且稳定的自监督学习(模型,代理任务…)
- 预训练方法在所有下游任务上都有效(对比偏好分类,MAE偏好生成任务…)
- 如何简单有效地拓展模型(ViT大规模自监督训练易崩溃,Mamba拓展性问题)
自回归预训练
NLP中的自回归预训练
NLP中的自回归是对语料库(句子)U={u1,…,un}中下一个单词的概率的预测:
p(u)=i=1∏np(ui∣u1,…,ui−1,Θ)
通过最小化负对数概率(最大化预测出句子的概率):
L=−logp(u)
视觉中带Mamba的自回归预训练
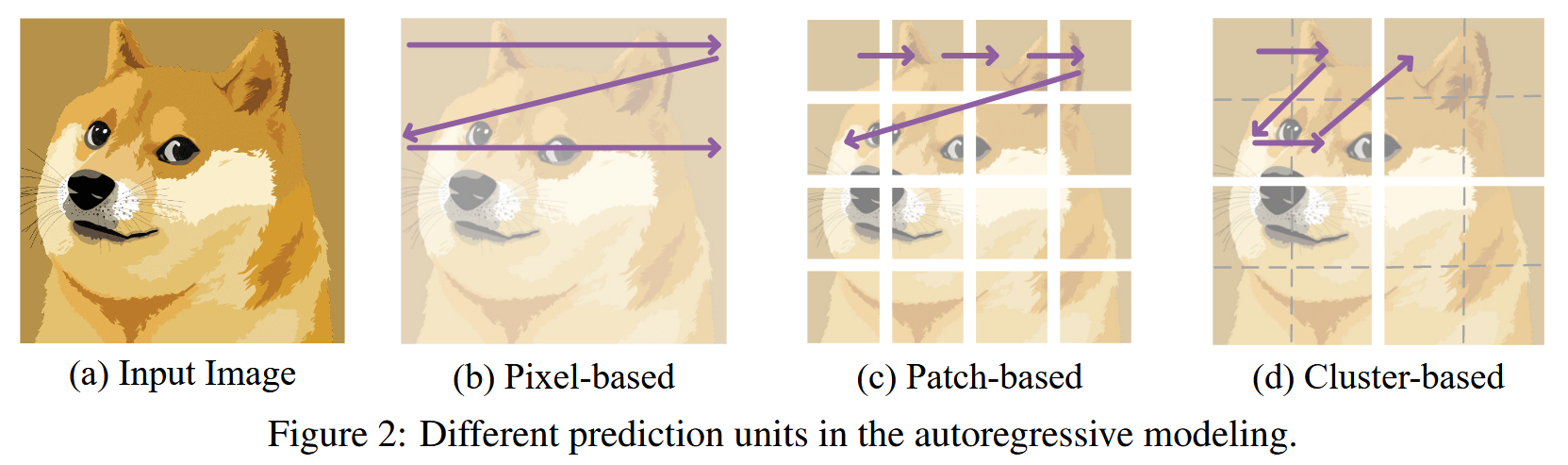
预测单位:
- 基于像素:首先需要定义2D中自回归的预测单位,iGPT定义为像素
L=i=1∑n−1l(f([p1,…,pi]),pi+1)l(y^,y)=∣y^−y∣2
其中,f(⋅)代表模型
这种基于像素的方法,引入了大量计算,在iGPT中,就使用了低分辨率的图像
基于patch:将图像切分为不重叠的patch,并转换为视觉token
L=i=1∑n−1l(f([P1,…,Pi]),Pi+1),l(y^,y)=∣y^−y∣2.
基于patch簇的:将空间上邻近的patch组成更长的token
LARMl(y^,y)=i=1∑n−1l(f([c1,…,ci]),ci+1)=∣y^−y∣2
预测顺序:
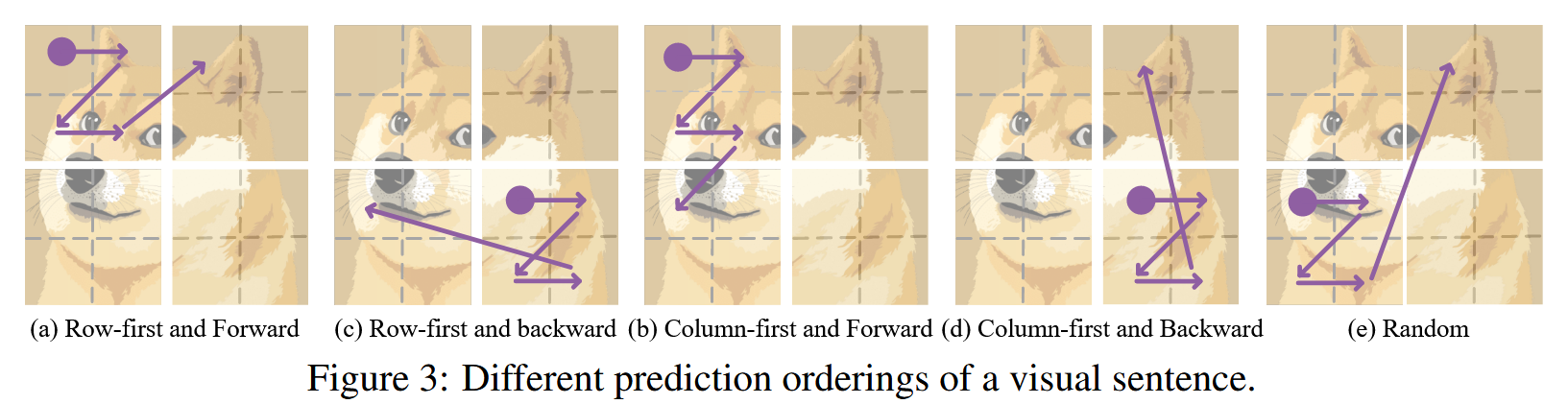
对于将2D图像变换为1D序列后如何决定预测顺序,但更多是以实验为主,缺乏相关的理论依据
MambaMLP
由Transformer Block启发而来,在预训练和微调阶段不同,将Mamba块用作于token混合,MLP用作于通道混合:
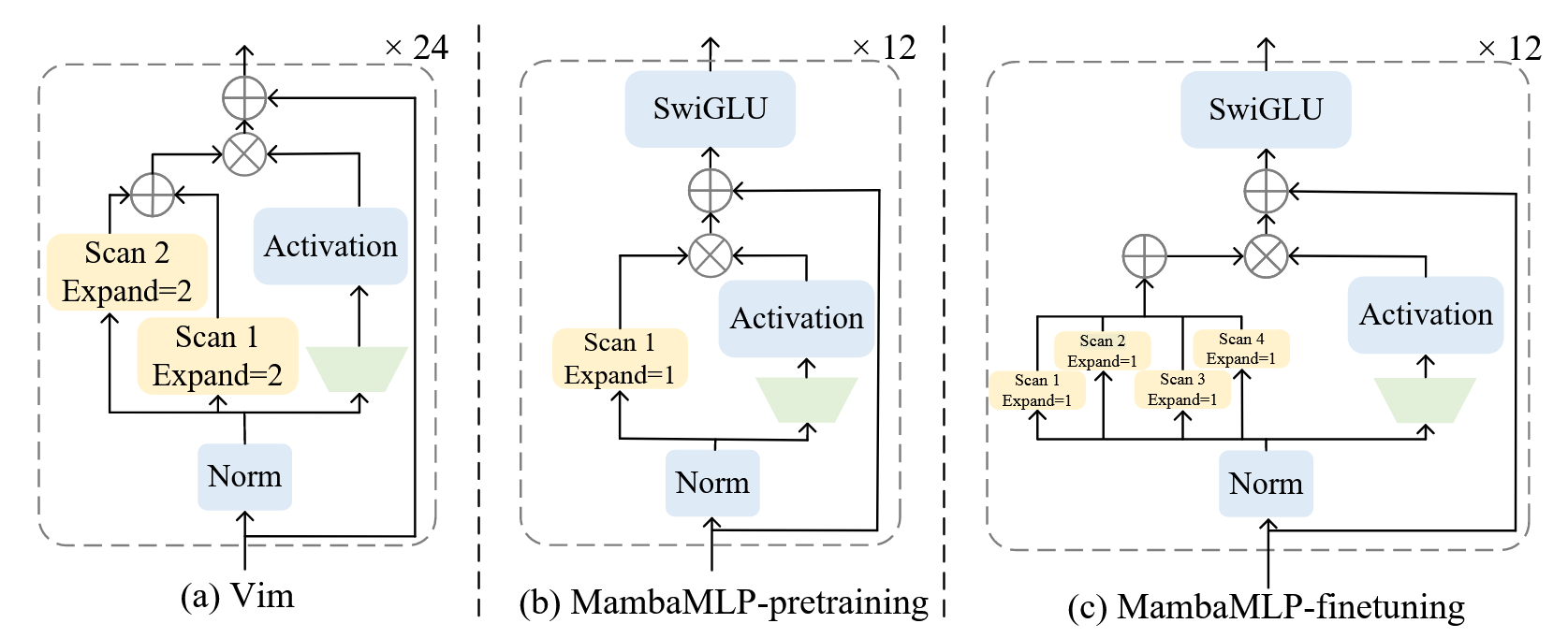
在预训练阶段,只有一次扫描来符合自回归的单方向,在微调阶段,使用4个方向的扫描,类似于VMamba中的双向扫描来获取全局信息
扫描的expand参数设定为1,Vim使用expand参数为2
expand参数越大,性能更好,但推理速度更慢
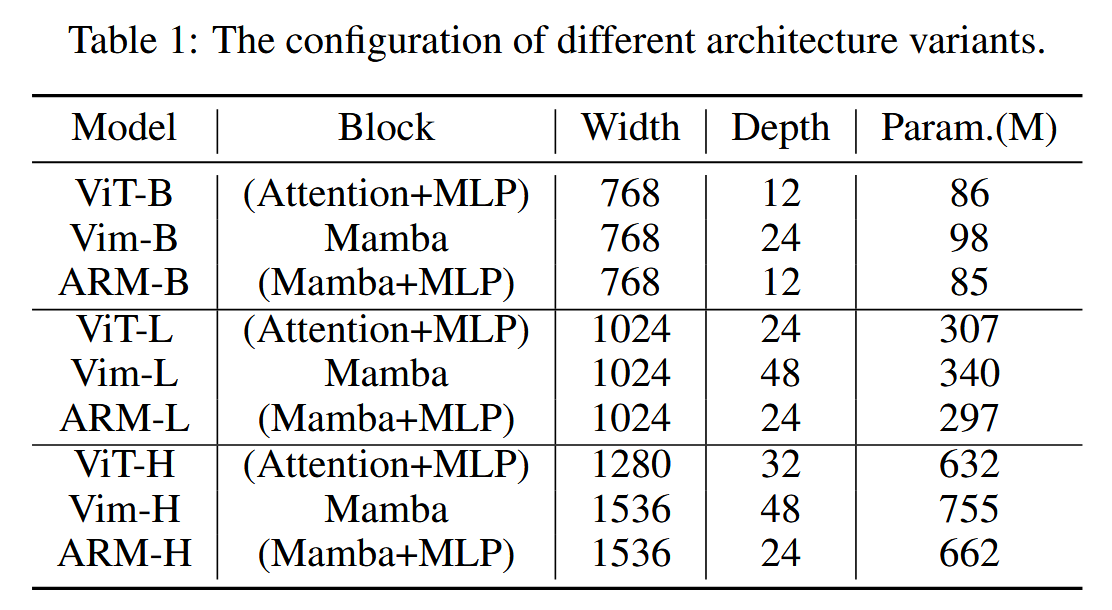
实验
实验设定
在ImageNet-1k上预训练,ARM-B和ARM-L为1600epoch,ARM-H为800epoch,batch分别为2048,1024,512,lr为1.5e−4×256 batchsize ,余弦退火策略,warm-up为5epoch,AdamW优化器输入为192×192,使用随机裁剪和flipping
在ImageNet分类上进行微调,100epoch,batch1024,输入为224×224,增强与MAE相同,AdamW,lr=5e−4×256 batchsize ,余弦退火策略,warm-up为5epoch,使用了EMA
在ImageNet的变体上进行了测试,包括自然增强(ImageNet-A),语义变化(ImageNet-R),骨架(ImageNet-S),ImageNet-V2,ImageNet-Real
对比实验
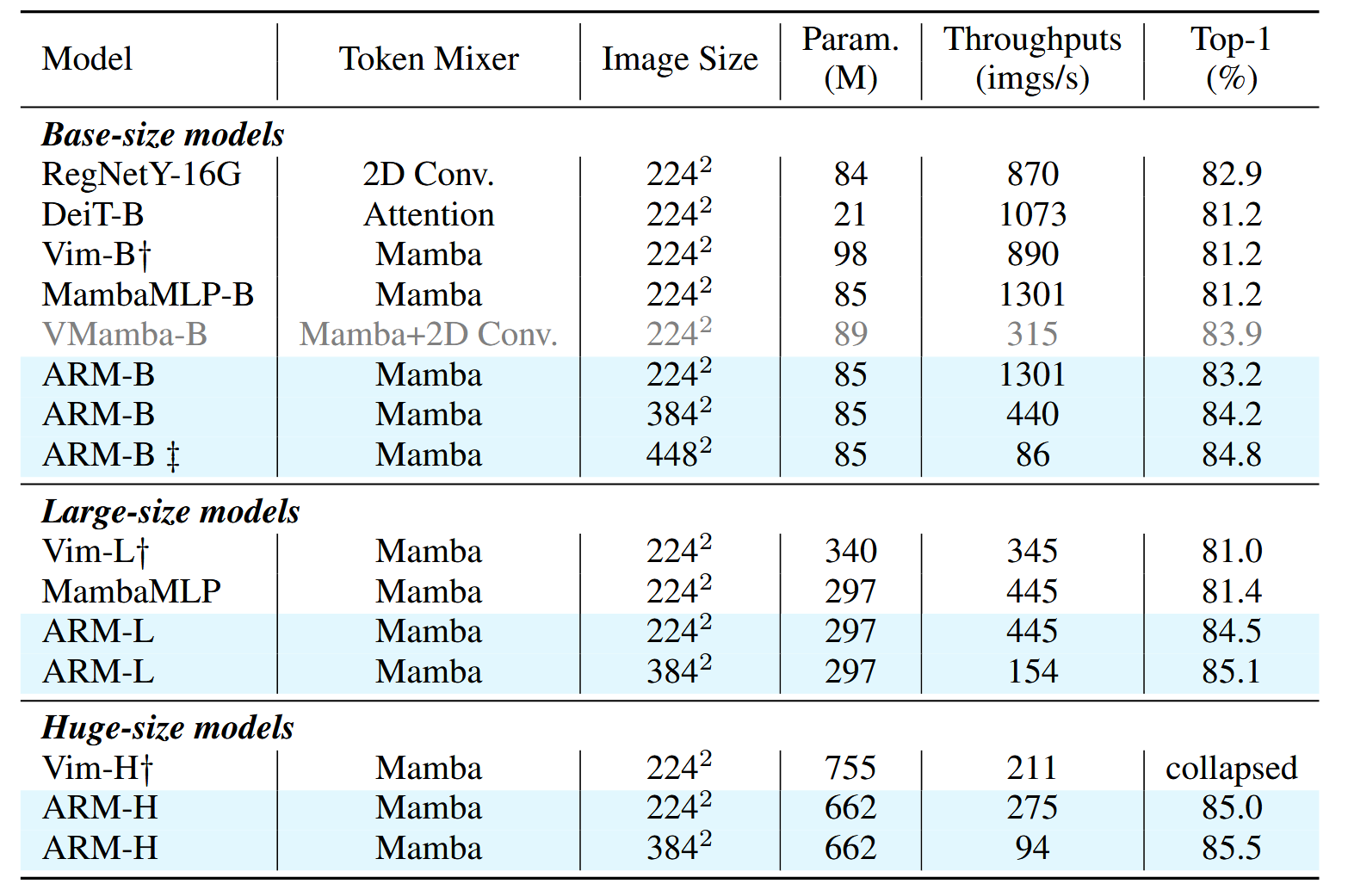
其它模型没有采用了自监督预训练
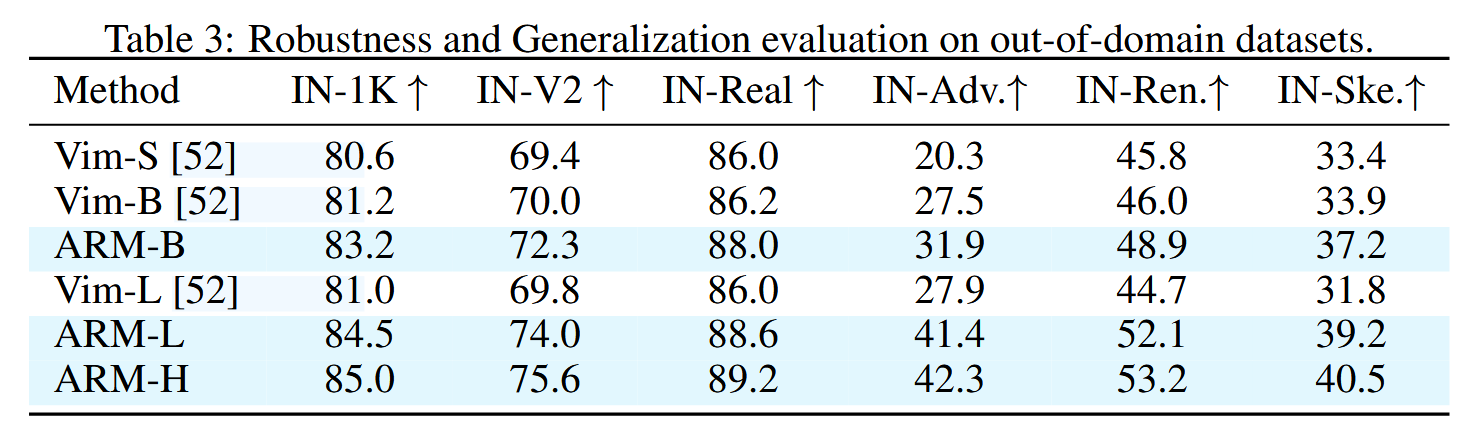
消融实验
簇中patch的消融:
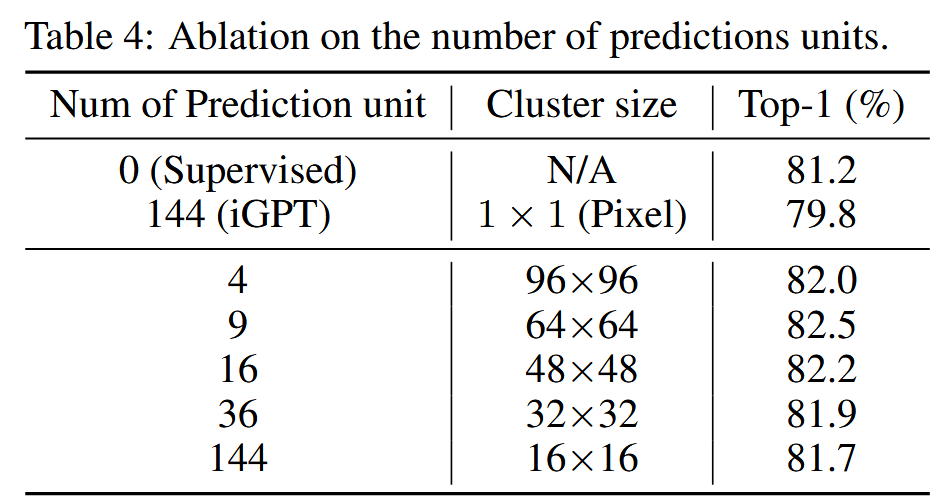
预测顺序:
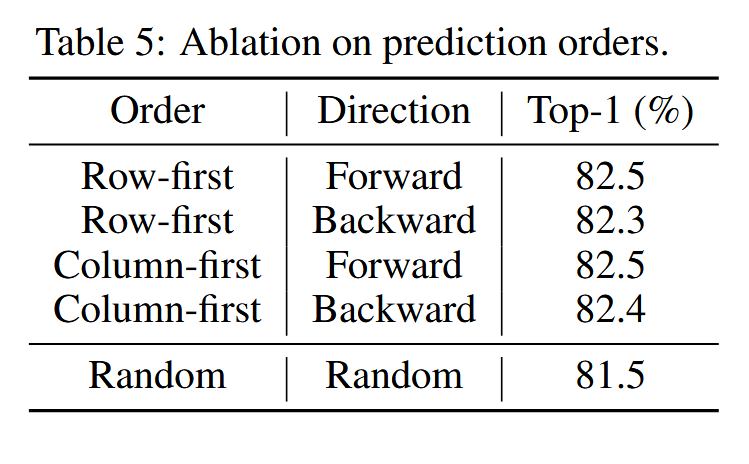
Decoder设计:
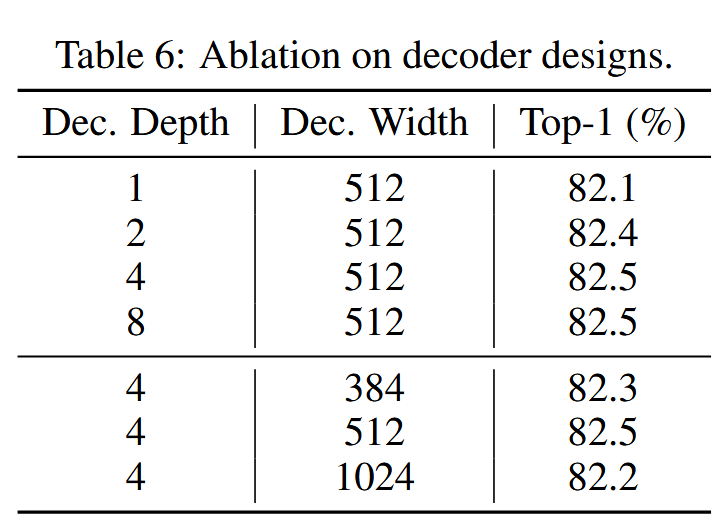
目标设计:
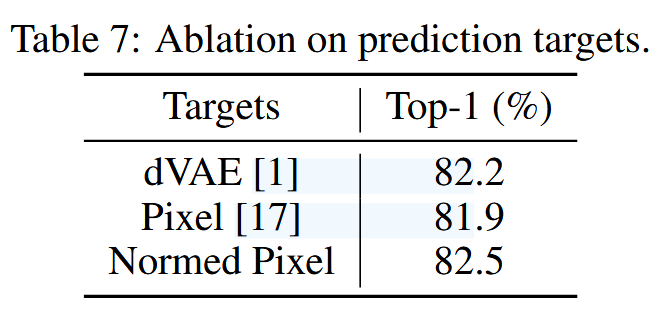
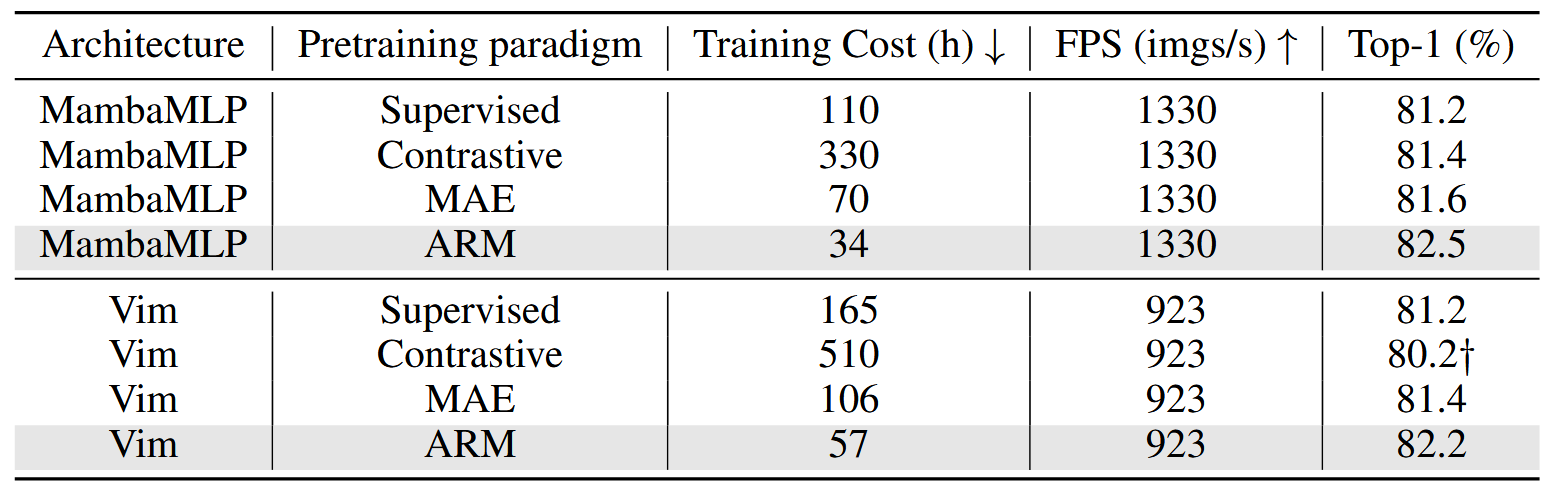
不同的代理任务:
总结
文章探索了自回归预训练与Mamba模型结合的训练,探索视觉Mamba架构的自监督范式,然而:
- 视觉自回归方法缺乏理论基础或者直觉经验
- 性能和拓展性仍比不上最新的ViT结构
















