背景
Title: BitNet: Scaling 1-bit Transformers for Large Language Models
Author: Hongyu Wang, Shuming Ma, Li Dong, Shaohan Huang, Huaijie Wang, Lingxiao Ma, Fan Yang, Ruiping Wang, Yi Wu, Furu Wei
Publish: arxiv
Year: 2023
Code: https://github.com/microsoft/BitNet
Keyword: 量化,Transformer,大模型
信息
现有的大部分量化方法都是后训练的,然而,尤其是在准确率较低的情况下,它们的性能不好
即在训练时没有为量化表示优化,有一些像大模型没有冗余和留有余力
另一种是是quantization-aware training,可以取得更好的性能,可以继续训练或者微调,但难以训练,并且是否遵循scaling law
以往对于有一些研究,但:
bert的encoder-decoder等模型没有展现出scaling law
贡献:
- 提出了BitNet,一个1bit transformer结构,在训练时,权重和激活函数使用低精度,优化器状态和梯度使用高精度
- 可以scale且具有较高的稳定性
- 模型相对简单,对于
nn.Linear进行重构,并且,引入了诸如PagedAttention,FalshAttention,speculative decoding
方法
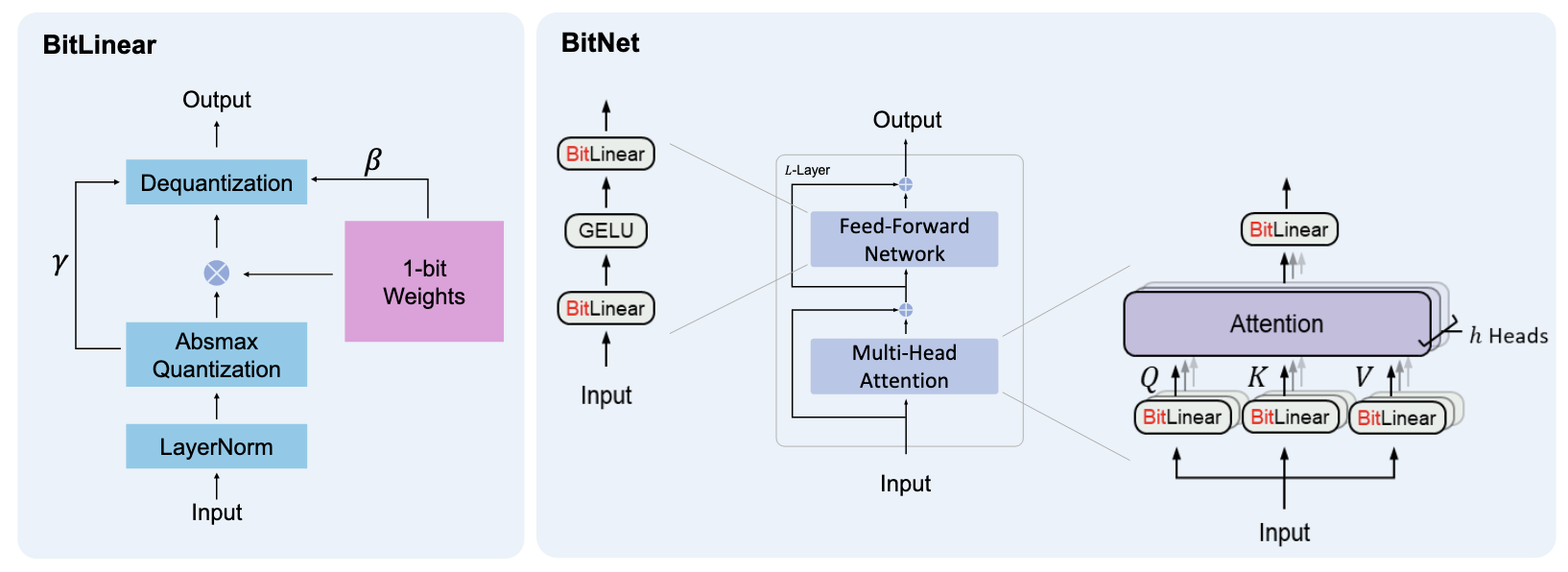
BitNet结构与transformer类似,只是使用BitLinear改写了所有线性层,保留了其它为高精度:
- 残差连接和layer normlization对于LLM来说计算量很少
- QKV的计算比参数映射少很多
- 保留了输入/输出,来进行采样
BitLinear
权重二值化
首先用符号函数sig将权重二值化,具体来说:
W=Sign(W−α),Sign(Wij)α={+1,−1, if Wij>0, if Wij≤0,=nm1ij∑Wij
- 将权重中心化为均值为0,即减α,尽量平衡容量
- 进行二值化
- 使用一个缩放系数β来缩小真值和二值化后的L2损失
输入b-bit化
作者称这一步为激活?
使用最大值缩放,即将激活值缩放到[−Qb,Qb](Qb=2b−1)之间:
x=Quant(x)=Clip(x×γQb,−Qb+ϵ,Qb−ϵ),Clip(x,a,b)=max(a,min(b,x)),γ=∥x∥∞,
其中,ϵ是防止Clip时溢出的极小值
特别的,对于在非线性激活层之前的,通过减去均值将其缩放到[0,Qb]之间:
x=Quant(x)=Clip((x−η)×γQb,ϵ,Qb−ϵ),η=ijminxij.
TODO: why
一些细节:b=8,且训练时针对每个tensor,推理时针对每个token
归一化
由此,BitLinear可以写成:
y=Wx
假设W和x中的元素是独立同分布的,且W和x相互独立,那么y的方差就是:
Var(y)=nVar(wx)=nE[w2]E[x2]=nβ2E[x2]≈E[x2]
对于全精度训练,由于标准初始化(kaiming init, Xavier init等)会把输出的方差缩放到1
为了在量化之后方差还为1,量化之前加入了LayerNorm
总体
总体公式就为:
y=Wx=WQuant(LN(x))×QbβγLN(x)=Var(x)+ϵx−E(x),β=nm1∥W∥1
组并行化
现有的模型并行化都是基于在切分维度上张量是独立的,但这里的α,β,γ,均值,方差等是由整个张量计算
尽管可以使用all-reduce的方案,但同步过程太大
将权重和激活值分成不同的组,形成Group Quantization,一个权重分为G组,一组有Gn×m个参数,然后在组间并行:
αg=nmGij∑Wij(g),βg=nmGW(g)1
同样,也对于输入分为G组:
γg=x(g)∞,ηg=ijminxij(g)
而LN也是:
LN(x(g))=Var(x(g))+ϵx(g)−E(x(g))
训练
Straight-through estimator
使用STE估计越过不可微的部分(符号函数,Clip等)
混合精度训练
梯度和优化器状态仍然使用高精度来保证稳定性和准确度,并为高精度的可学习参数维护了一个潜在状态来累计参数更新,其在训练时为二值,在推理时不使用
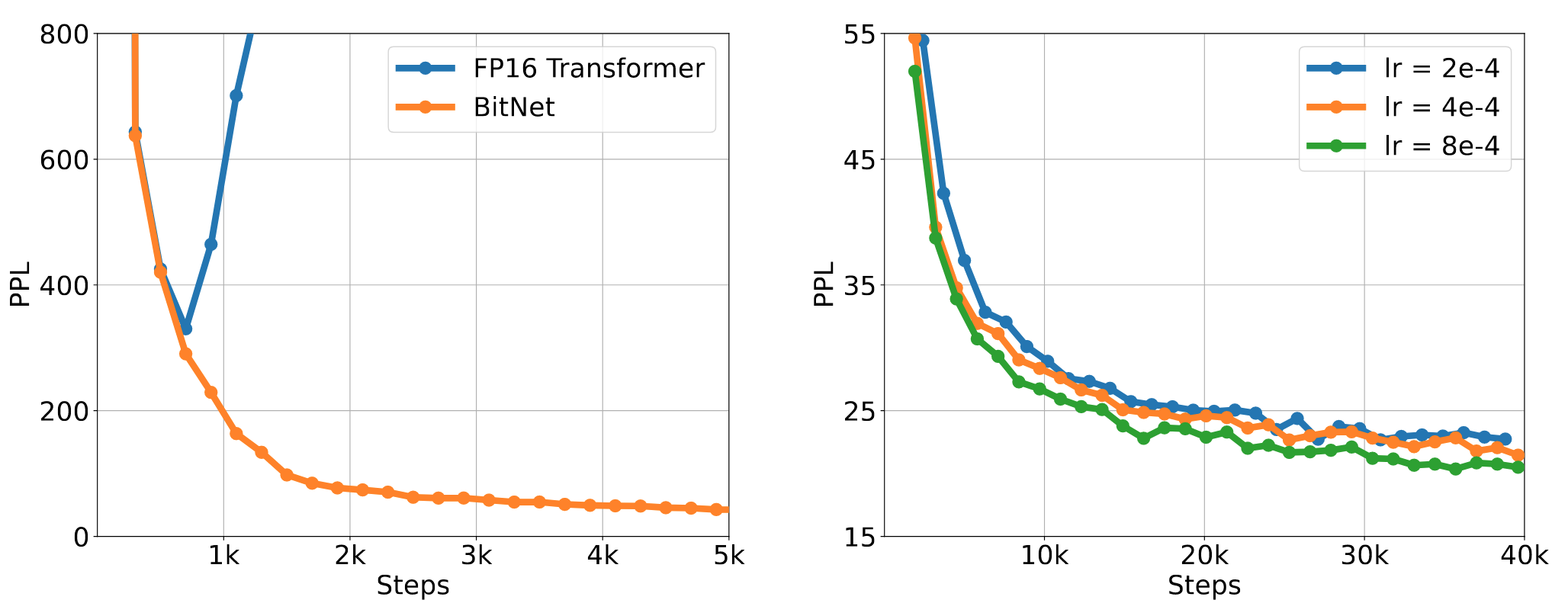
大学习率
通常,对于潜在权重的小的更新通常不起作用
大学习率对于二值网络收敛非常重要
计算效率
不同节点乘加的效率:
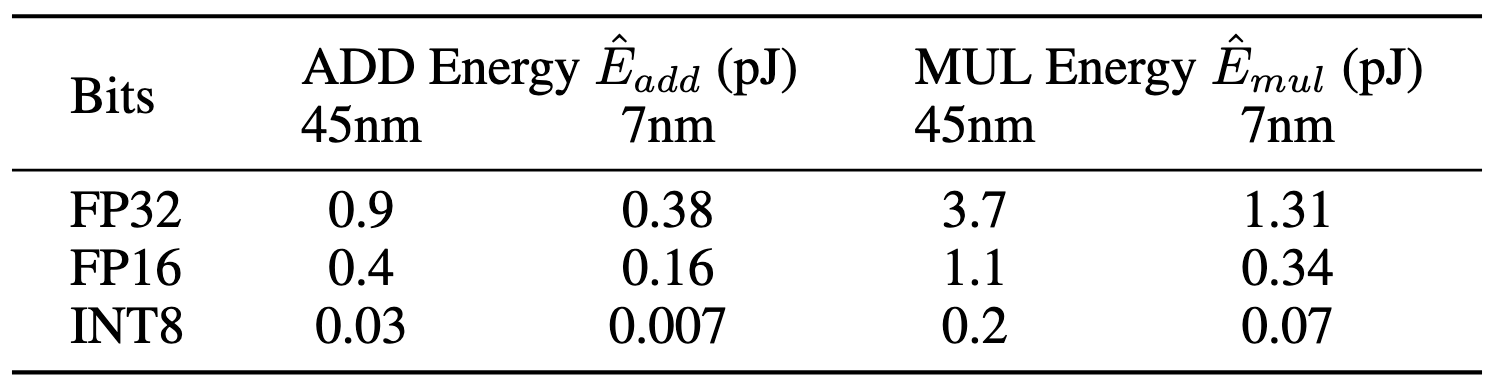
对于原始transformer,其能量消耗是:
EaddEmul=m×(n−1)×p×E^add=m×n×p×E^mul
对于BitNet,由于是1bit,只有1或-1,主要运算为加法,能量消耗为:
Emul=(m×p+m×n)×E^mul
实验
实验设定
训练了不同大小的BitNet(从125M到30B)
数据集为英文资料文集,包括Pile,Common Crawl snapshots,RealNews,CC-Stories
使用了Sentencpiece序列化器,词表大小为16K
推理最佳scaling law
大致符合公式:
L(N)=aNb+c
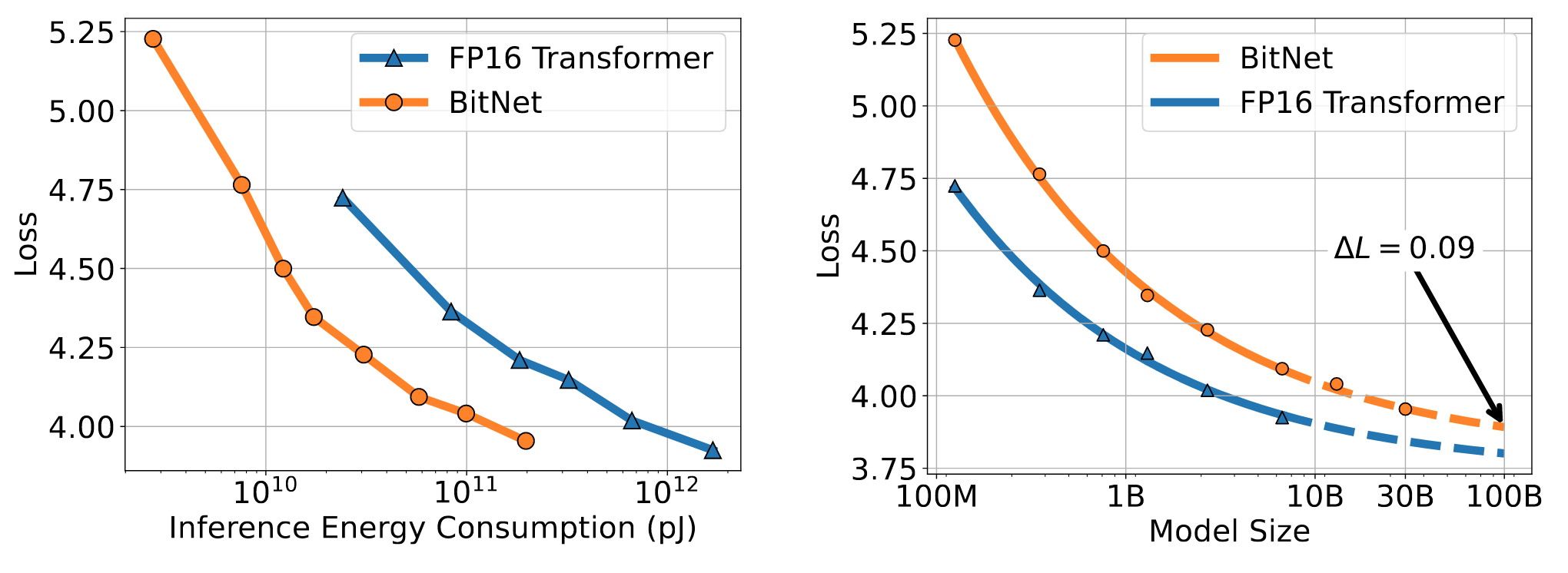
以往的计算量计算方法不适合于BitNet,提出了Inference-Optimal Scaling Law,是用能量来计算
下游任务
使用了0-shot和4-shot
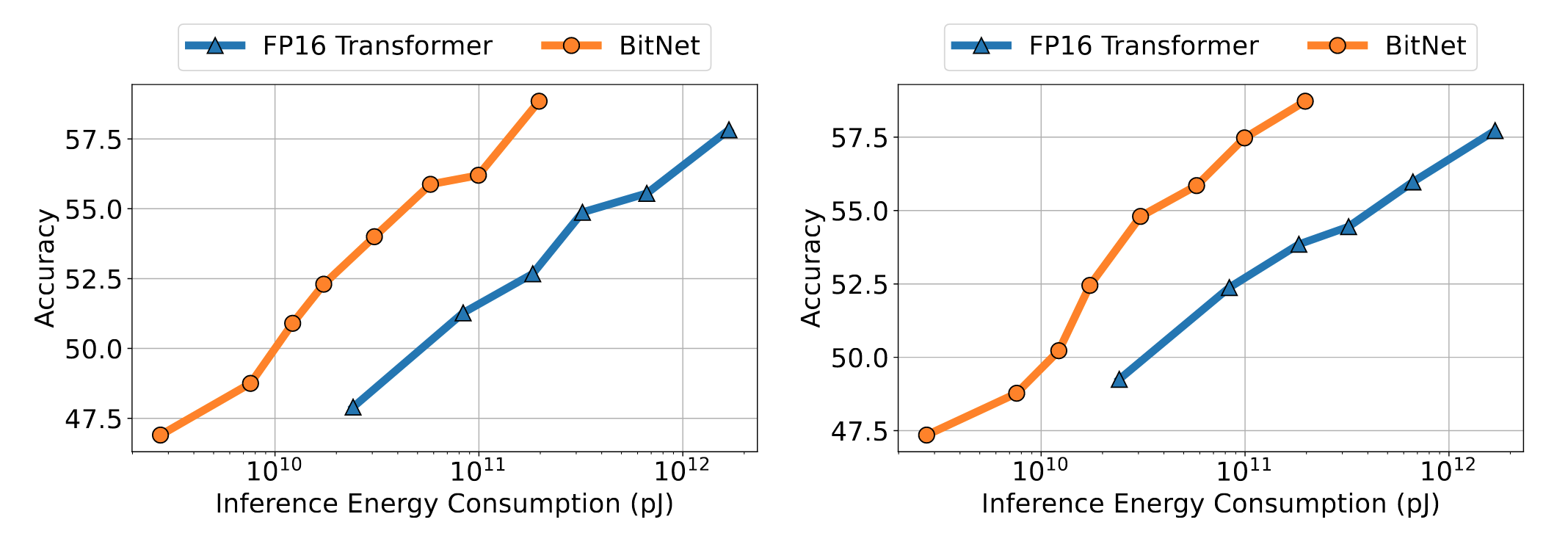
稳定性
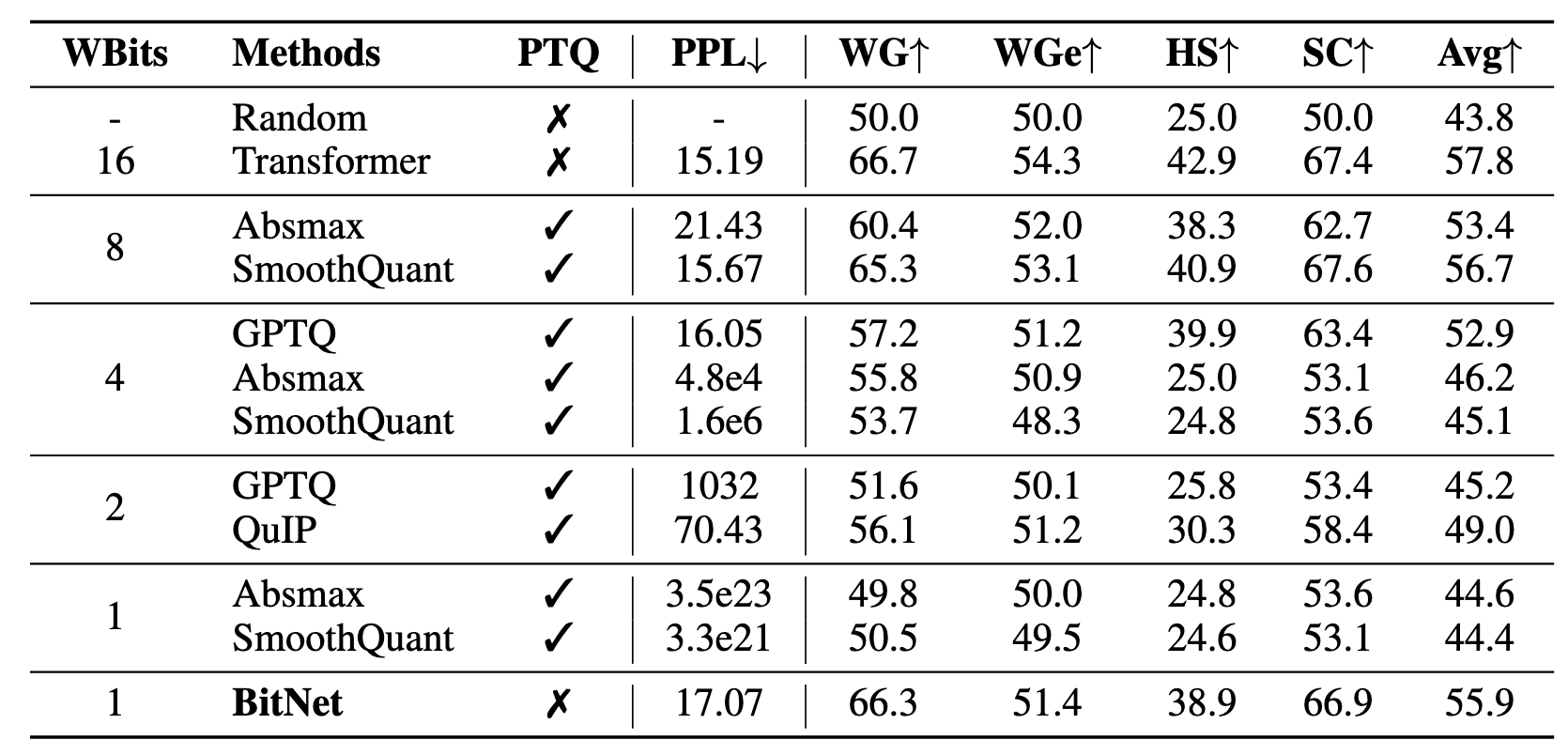
与后训练量化对比
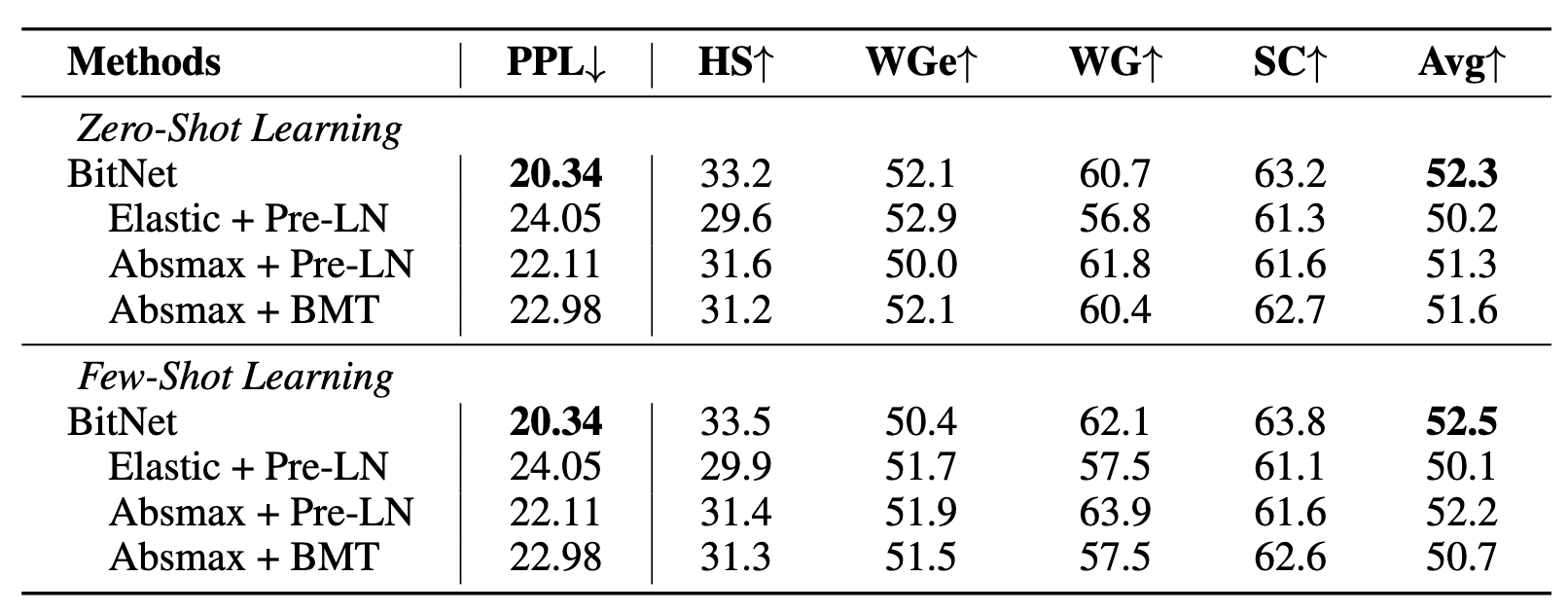
消融实验
总结
探究了如何从头训练一个量化的网络,提出了构建Transformer的基础bit结构:
- 构建了稳定的bit线性层计算和训练,模型可以在此基础上进行拓展
- 证明了bit结构下,可以在性能不损失过多的情况下,显著减少计算资源消耗
- 证明bit结构下,模型也可以符合scaling law
然而:
- 实验最大参数量只有8B,更多参数量性能为预估值
- 下游任务相对简单






