信息

Title: BitNet v2: Native 4-bit Activations with Hadamard Transformation for 1-bit LLMs

Author: Hongyu Wang, Shuming Ma, Furu Wei

Year: 2025

Publish: arxiv

Code: https://github.com/microsoft/BitNet

Keyword: 量化，Transformer，大模型

背景

现代GPU对于低精度有更好的支持，例如GB200原生支持4bit

BitNet b1.58可以实现近乎和全精度类似的性能，但保留了8bit激活值，没有发挥出全部潜力

低精度激活值的难点在于LLM中激活值的非均匀分布(虽然能在Attention和FFN中保持类高斯分布，但中间状态，即在最终映射前的输出会含有极端值)

BitNet a4.8尝试使用对输入4bit量化和中间状态8bit稀疏化来解决问题，但稀疏化不利于高效推理

贡献：

提出了 $\mathcal{H}$ -BitLinear，在激活值量化之前使用了一个在线哈曼德变换，在整个模型实现了原生4bit
实现了BitNet v2，利用8bit激活值进行训练，实现了和BitNet b1.58类似的性能，模型可以用4bit激活值进行微调

方法

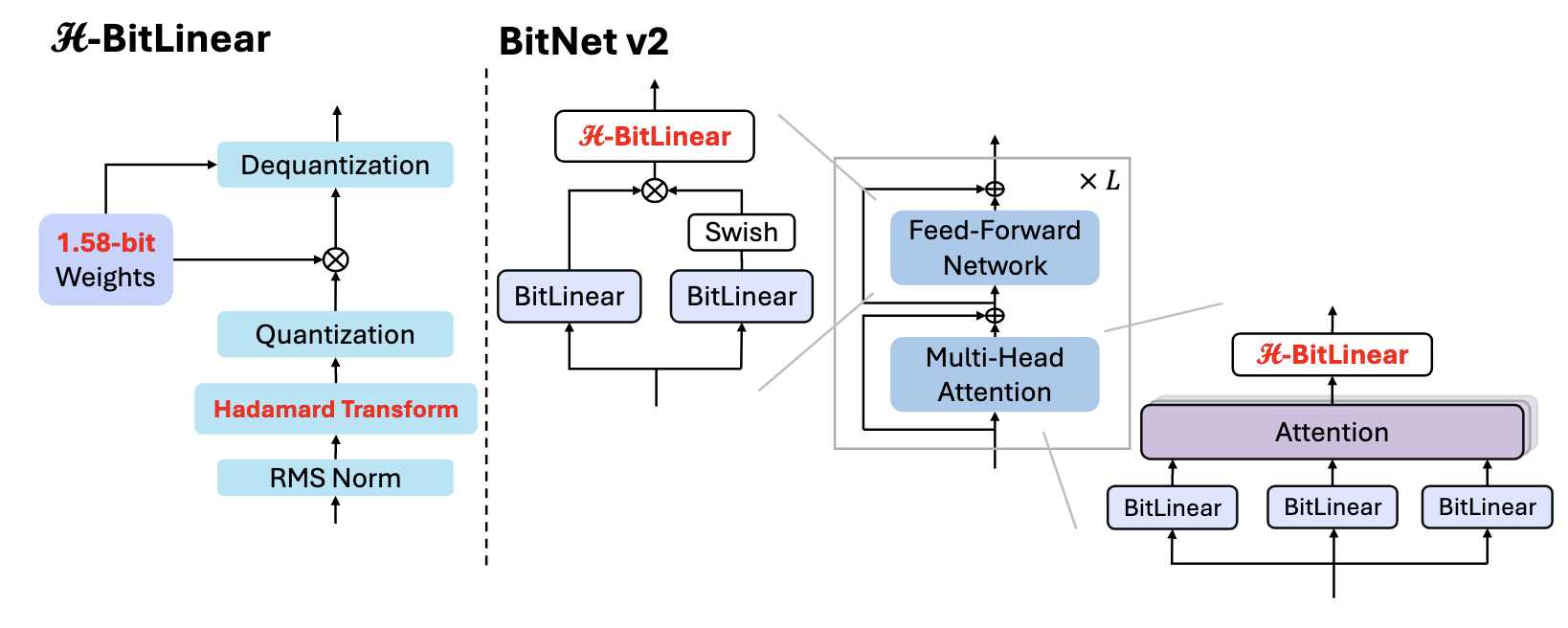
整体上，采用了LLAMA类似的方法，例如RMS norm，SwishGLU，不使用偏置项，在attention的 $W_o$ 和FFN中的 $W_{down}$ 中引入了 $\mathcal{H}$ -BitLinear层

原生4-bit激活值

权重量化

针对于每个tensor，使用 $absmean$ 将权重量化为三进制值{-1, 0, 1}：

对比二进制？

$\begin{aligned} & \mathrm{Q}_w(\mathbf{W})=\alpha \operatorname{RoundClip}\left(\frac{\mathbf{W}}{\alpha+\epsilon},-1,1\right), \alpha=\operatorname{mean}(|\mathbf{W}|) \\ & \operatorname{RoundClip}(X, a, b)=\min (\max (\operatorname{round}(X), a), b) \end{aligned}$

即把大于mean的映射到1，小于-mean的映射到-1，在[-mean, mean]之间的映射到0

$\mathcal{H}$ -BitLinear

之前的工作揭示了attention和FFN的输入(即 $W_{qkv}$ 和 $W_{up,gate}$ 的输入)是类高斯分布，然而中间态的输入(即 $W_o$ 和 $W_{down}$ 的输入)会有大量异常值(大量极端值和接近0的值)，由此，作者针对 $W_o$ 和 $W_{down}$ 引入了 $\mathcal{H}$ -BitLinear

具体来说，在激活值进行量化前，首先引入哈曼德变换来减少离群值：

$\begin{aligned} & \text { Hadamard }(\mathbf{X})=\mathbf{H}_{\mathbf{m}} \mathbf{X} \\ & \mathbf{H}_{\mathbf{m}}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc} \mathbf{H}_{\mathbf{m}-\mathbf{1}} & \mathbf{H}_{\mathbf{m}-\mathbf{1}} \\ \mathbf{H}_{\mathbf{m}-\mathbf{1}} & -\mathbf{H}_{\mathbf{m}-\mathbf{1}} \end{array}\right), \mathbf{H}_{\mathbf{0}}=(1) \end{aligned}$

其中， $H_m$ 是一个 $2^m \times 2^m$ 的矩阵，假设 $X\in R^n$ ， $n=2^m$ 。在这里，使用了快速哈曼德变换，有 $\mathcal{O}(n \log n)$ 的复杂度。

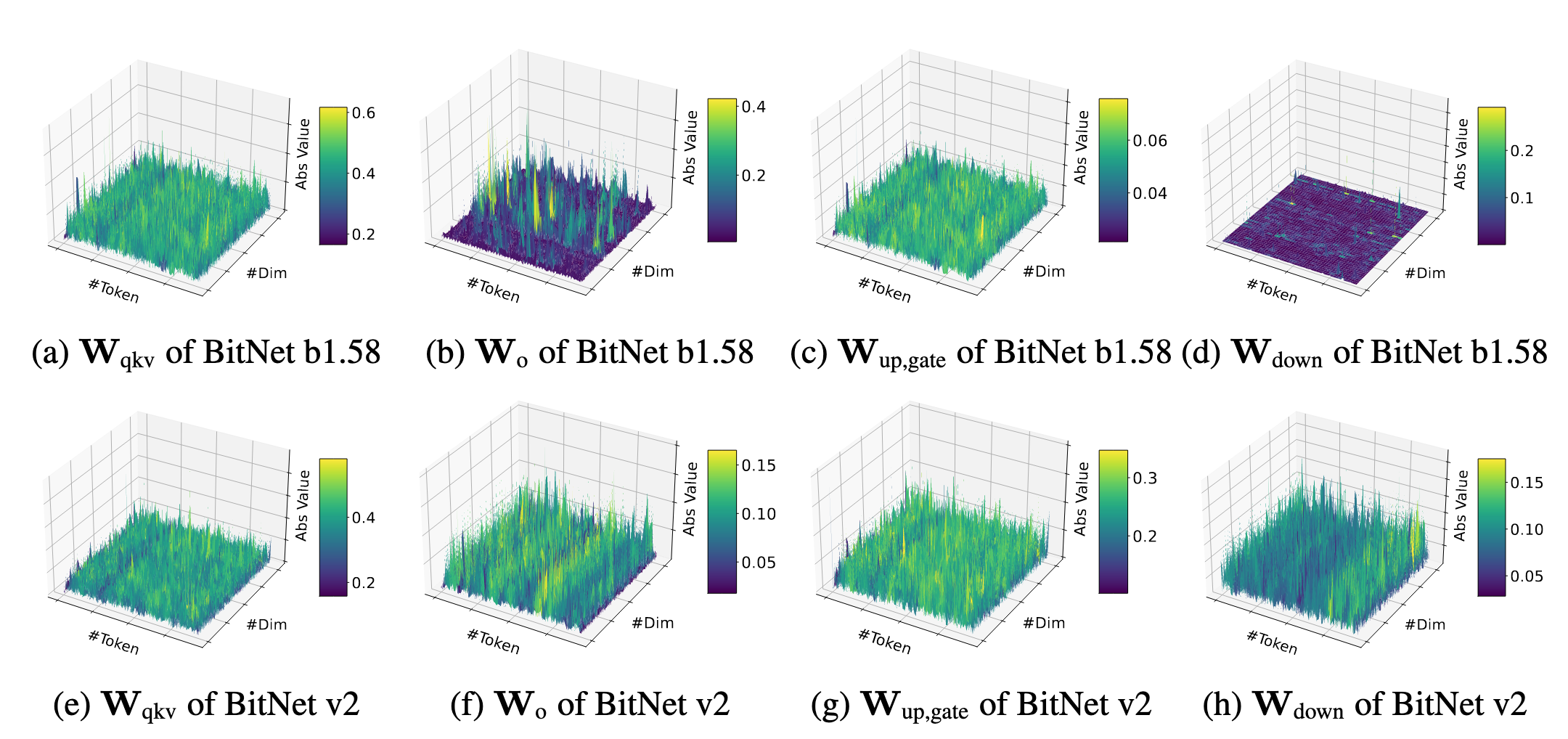
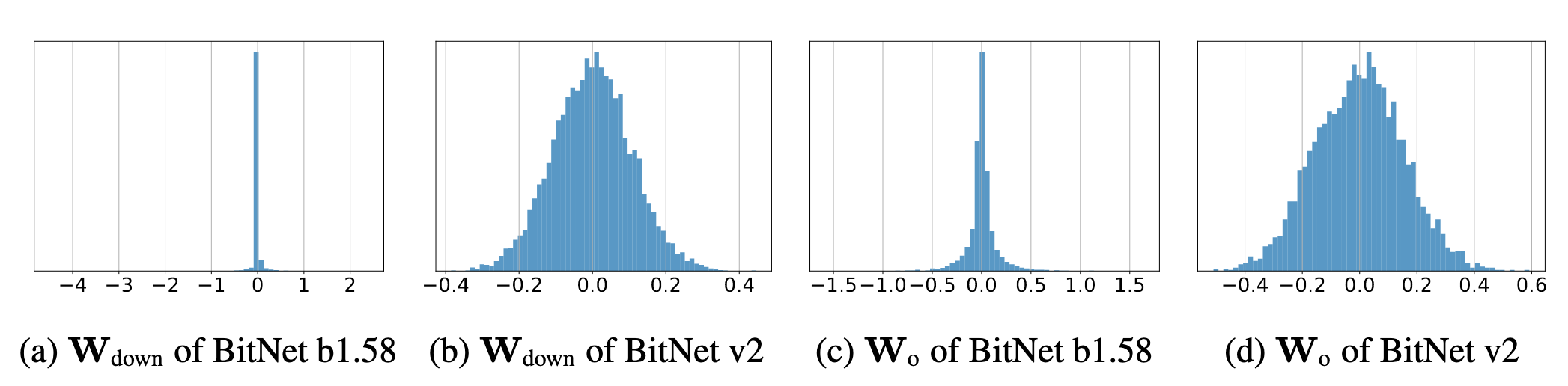
这会使得权重和激活值更类似于高斯分布，更适合INT4量化

对于激活值的8-bit和4-bit量化，就可以使用token级的absmax和absmean完成：

$\begin{aligned} & \mathrm{Q}_{\mathrm{INT} 8}(\mathbf{X})=\frac{\gamma}{127} \operatorname{RoundClip}\left(\frac{127}{\gamma+\epsilon} \mathbf{X},-128,127\right), \gamma=\max (|\mathbf{X}|) \\ & \mathrm{Q}_{\mathrm{INT} 4}(\mathbf{X})=\frac{\beta}{\sqrt{7}} \operatorname{RoundClip}\left(\frac{\sqrt{7}}{\beta+\epsilon} \mathbf{X},-8,7\right), \beta=\operatorname{mean}(|\mathbf{X}|) \end{aligned}$

给出 $\mathcal{H}$ -BitLinear的公式就是：

$\mathbf{Y}=\mathrm{Q}_w(\mathbf{W}) \cdot \mathrm{Q}_{\mathrm{INT} 8 / 4}\left(\mathbf{X}_{\mathbf{r}}\right), \mathbf{X}_{\mathbf{r}}=\operatorname{Hadamard}(\mathrm{LN}(\mathbf{X}))$

训练

同样，使用了straight-through estimator来进行梯度近似，并进行混合精度训练。在反向传播时，略过了不可微分的部分，并且，保留了全精度的梯度

尤其对于哈曼德变换的梯度，可以利用变换矩阵的正交性进行：

$\frac{\partial \mathcal{L}}{\partial \mathbf{X}}=\operatorname{Hadamard}\left(\frac{\partial \mathcal{L}}{\partial \operatorname{Hadamard}(\mathbf{X})}\right)$

并且，BitNet v2的4-bit的激活值可以在8-bit的基础上使用更少的训练token继续训练

实验

参数设定

使用了BitNet b1.58中的两阶段weight decay和学习率策略

实验条件

使用RedPajama数据集的100B的token

主要对比了BitNet b1.58和BitNet a4.8，所有模型都在1.58-bit上进行训练

BitNet b1.58对于所有线性层有完整的INT8激活值
BitNet a4.8在BitNet b1.58的基础上，利用混合量化和激活值的稀疏化进行继续训练，子层的输入进行4-bit量化，中间层的特征使用了top-K稀疏化和squared ReLU

实际上，BitNet a4.8和BitNet v2都是现在BitNet b1.58上训练(实验中是95B token)，然后在4-bit上继续训练

使用lm-evaluation-harness工具进行了零样本实验

结果

与之前改进对比

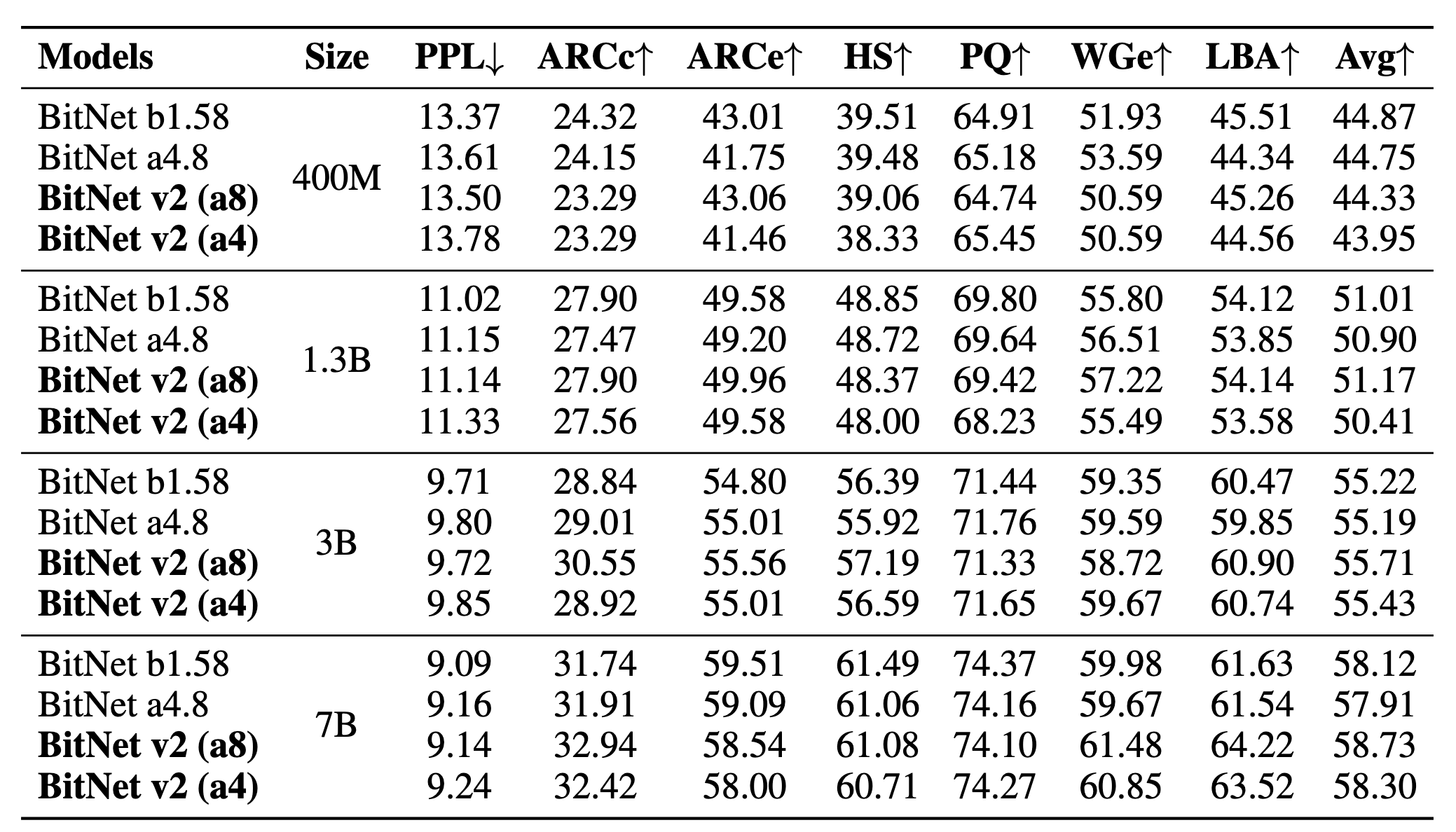
8-bit和4-bit对比

BitNet v2在RoPE之后进行量化，具有3位KV缓存的BITNET V2的精度可与3B和7B模型中的全精确kV缓存相媲美

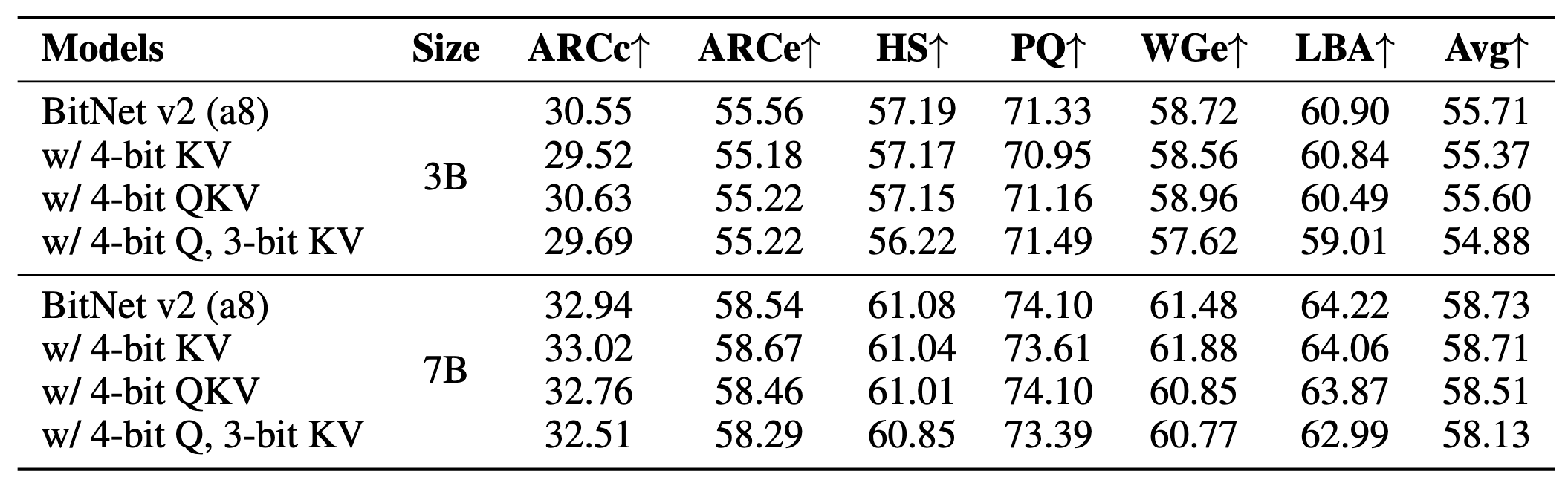
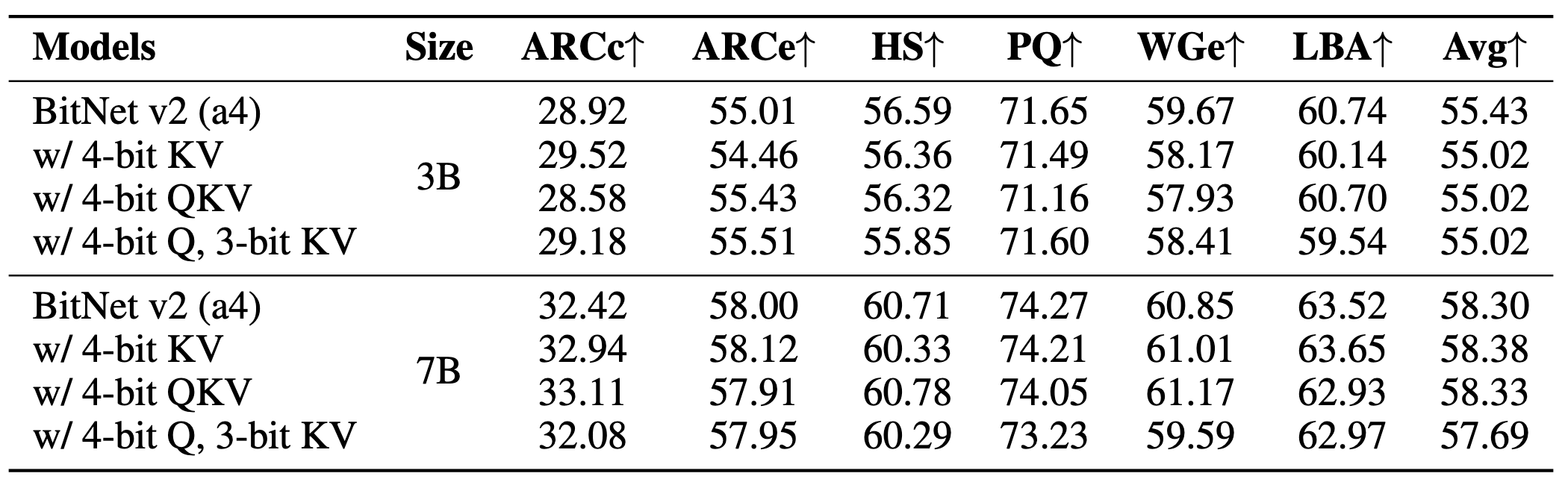
后训练量化对比

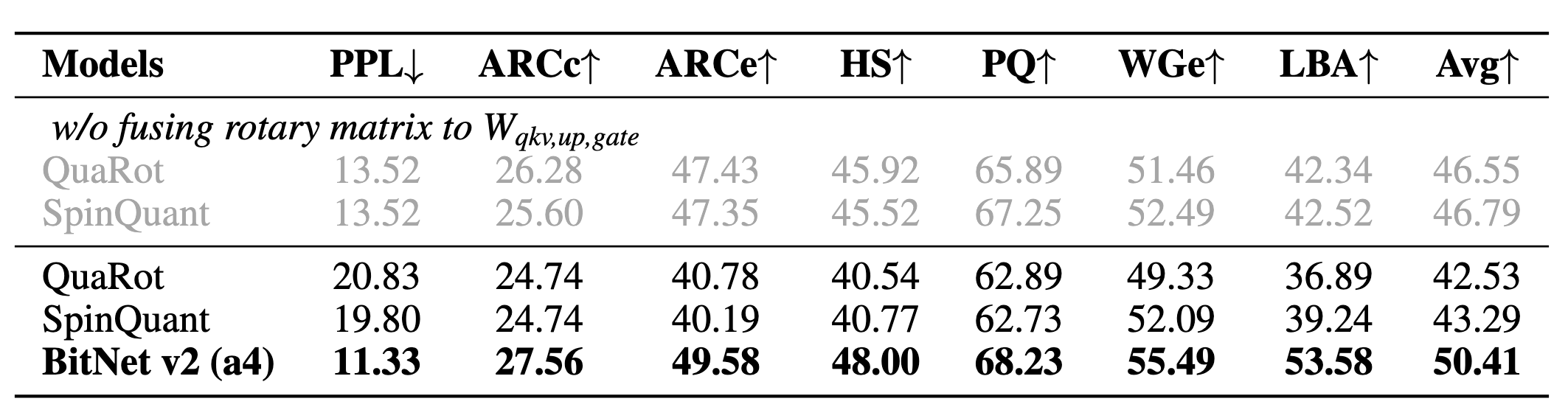
总结

和BitNet一样，探究了如何从头训练一个量化的网络，提出了构建Transformer的基础bit结构：

改进了bit结构下，中间层的激活值的非均匀分布问题
证明了bit结构下，可以在性能不损失过多的情况下，显著减少计算资源消耗
证明bit结构下，模型也可以符合scaling law

但还是之前的问题：

实验最大参数量只有8B，更多参数量性能为预估值
下游任务相对简单