[论文笔记] VAR

信息

Title: Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

Author: Keyu Tian, Yi Jiang, Zehuan Yuan, Bingyue Peng, Liwei Wang

Publish: NeurIPS

Year: 2024

Keyword: Autoregressive, self-supervised

Code: https://github.com/FoundationVision/VAR

关键词：自回归，Transformer，图像生成

背景

NLP中，LLM在泛化性和多样性上朝AGI更进一步，其核心在于自回归的自监督学习模型的可拓展性和泛化性(scaling law和零样本能力)

CV中，就尝试利用序列编码器将图像patch变为2Dtoken，并变为1D token做自回归，但拓展后性能不好，落后于扩散模型

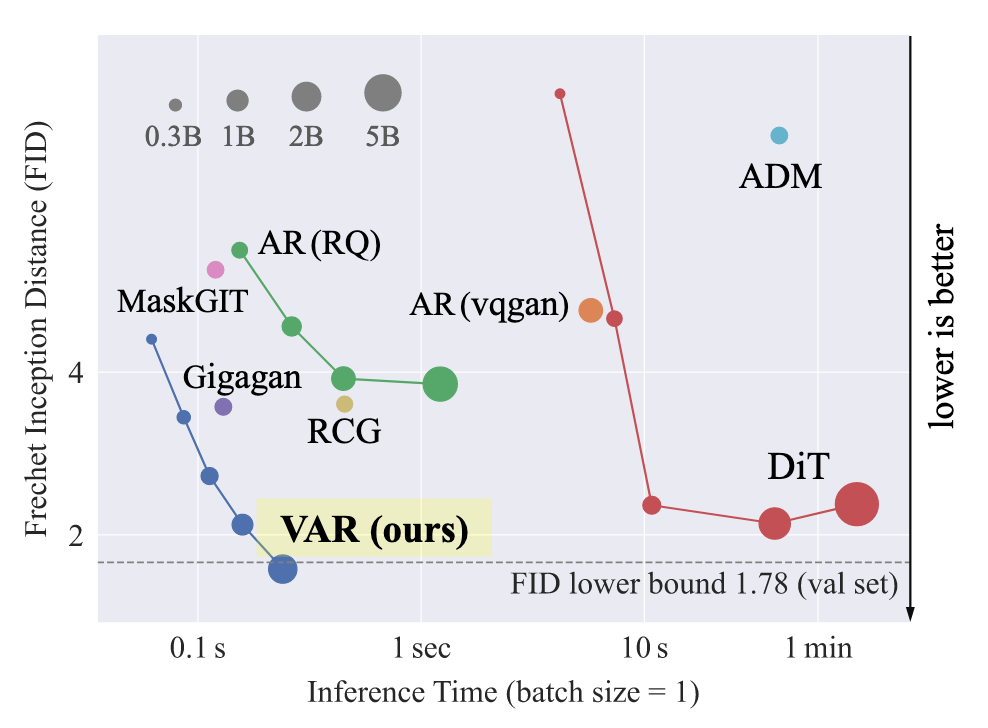
Frechet Inception distance是衡量生成模型生成质量的参数，衡量了整个数据集中生成图像和原始图像之间分布的距离（即一个数据集计算一个值）

计算中，首先两张图片先经过一个网络（一般为Inception v3），其符合高斯分布，然后对特征计算均值和方差，最终计算距离：

$$\mathrm{FID}=\left\|\mu_r-\mu_g\right\|^2+\operatorname{Tr}\left(\Sigma_r+\Sigma_g-2\left(\Sigma_r \Sigma_g\right)^{1 / 2}\right)$$

值得注意的是，FID是针对于整个数据集的指标，而非像LPIPS一样针对单张图像

Inception Score (IS)用于衡量生成图像的质量，主要标准为现实性和多样性，使用Inception v3分类模型衡量，现实性体现在能生成能使模型准确分类的图像，多样从模型能生成一系列类的图像而非一部分类

视觉基础模型：CLIP，SAM，Dinov2，提示工程：Painter，LVM

Raster扫描自回归：VQVAE，VQGAN，VQVAE-2，RQ-Transformer，Parti

掩码预测：MaskGIT，MagViT，MUSE

扩散模型：DiT，U-ViT，Stable diffusion，SORA，Vidu

自回归要点在于数据的顺序，人类一般多层次接受，首先看整体结构，然后逐渐关注细节信息

作者将视觉的自回归定义为下一个尺度的预测，Visual Autoregressive modeling

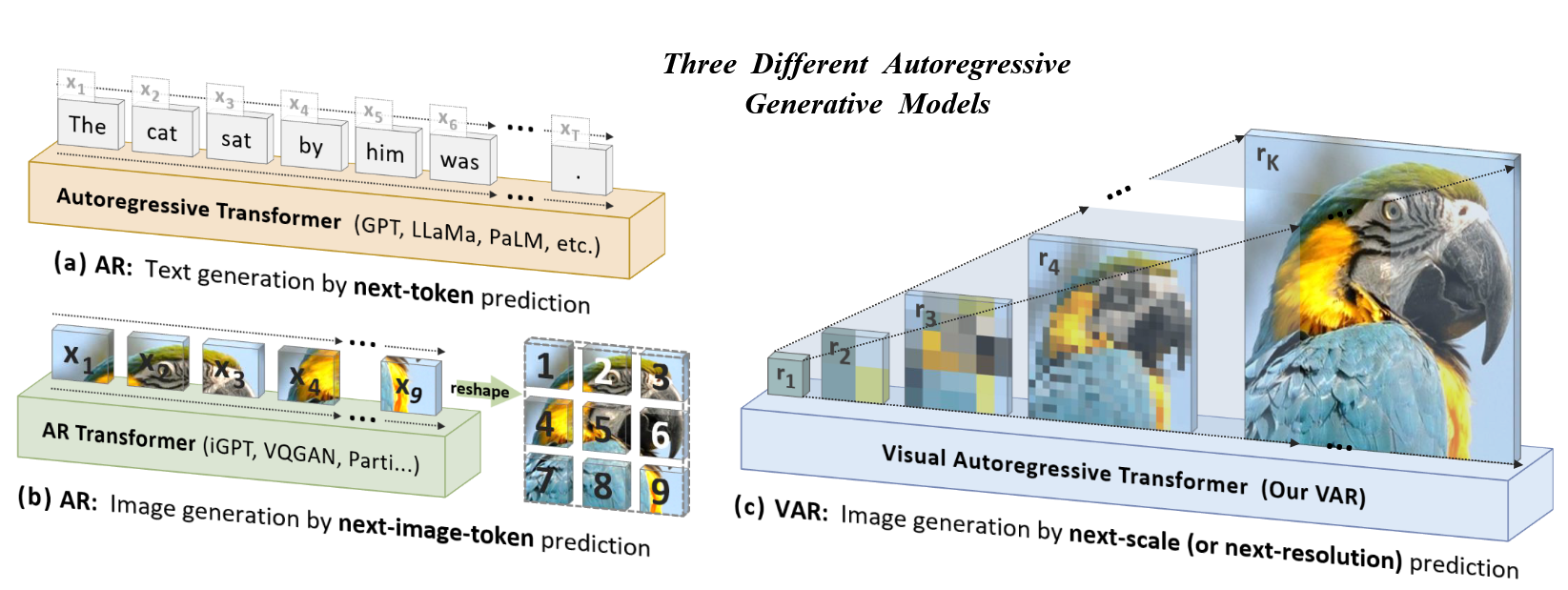
贡献：

• 提出了多尺度预测的自回归生成方式，由整体结构到细节信息进行预测
• 使用类似GPT-2的结构，实现多尺度视觉自回归
• 验证了模型的可拓展性和零样本能力

方法

前置信息：基于下个token预测的自回归

基于单项序列依赖的假设，序列$x$的可能性就可以因式分解：

$$p\left(x_1, x_2, \ldots, x_T\right)=\prod_{t=1}^T p\left(x_t \mid x_1, x_2, \ldots, x_{t-1}\right)$$

图像是2D连续信号，需要进行序列化，并决定顺序：

$$f=\mathcal{E}(i m), \quad q=\mathcal{Q}(f)$$

其中，im是原始图像，$\mathcal{E}(\cdot)$是编码器，$\mathcal{Q}(\cdot)$是序列化器，序列化器通常包含一个词典，会将特征向量映射到欧几里得空间中的编码序列：

$$q^{(i, j)}=\left(\underset{v \in[V]}{\arg \min }\left\|\operatorname{lookup}(Z, v)-f^{(i, j)}\right\|_2\right) \in[V]$$

由此，通过词书$Z$得到一个编号，并用decoder获取重建的图像，并计算损失：

$$\begin{aligned} & \hat{f}=\operatorname{lookup}(Z, q), \quad i \hat{m}=\mathcal{D}(\hat{f}) \\ & \mathcal{L}=\|i m-i \hat{m}\|_2+\|f-\hat{f}\|_2+\lambda_{\mathrm{P}} \mathcal{L}_{\mathrm{P}}(i \hat{m})+\lambda_{\mathrm{G}} \mathcal{L}_{\mathrm{G}}(i \hat{m}) \end{aligned}$$

其中，$\mathcal{L}_{\mathrm{P}}(\cdot)$是一个感性的损失，例如LPIPS，$\mathcal{L}_{\mathrm{G}}(\cdot)$是一个判别行损失

更像是encoder-映射-decoder来进行自回归

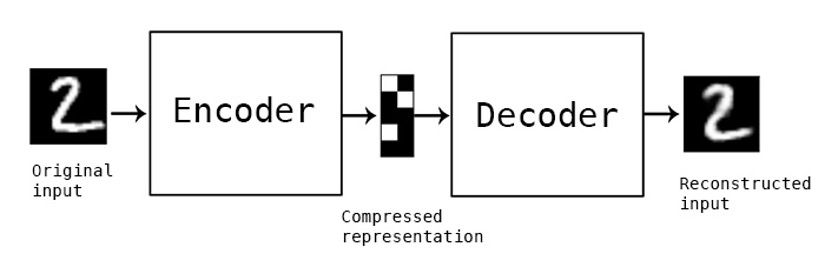
由此，自编码器$\{\mathcal{E}, \mathcal{Q}, \mathcal{D}\}$就可以进行单向自回归

缺点：

• 假设违背：这样产生的所有特征$f^{(i, j)}$，相互之间存在依赖，flatten之后就会有双向依赖，但对于自回归，建立在应该只有单向依赖上

  VQVAE的注意力分数图(1D token)

  

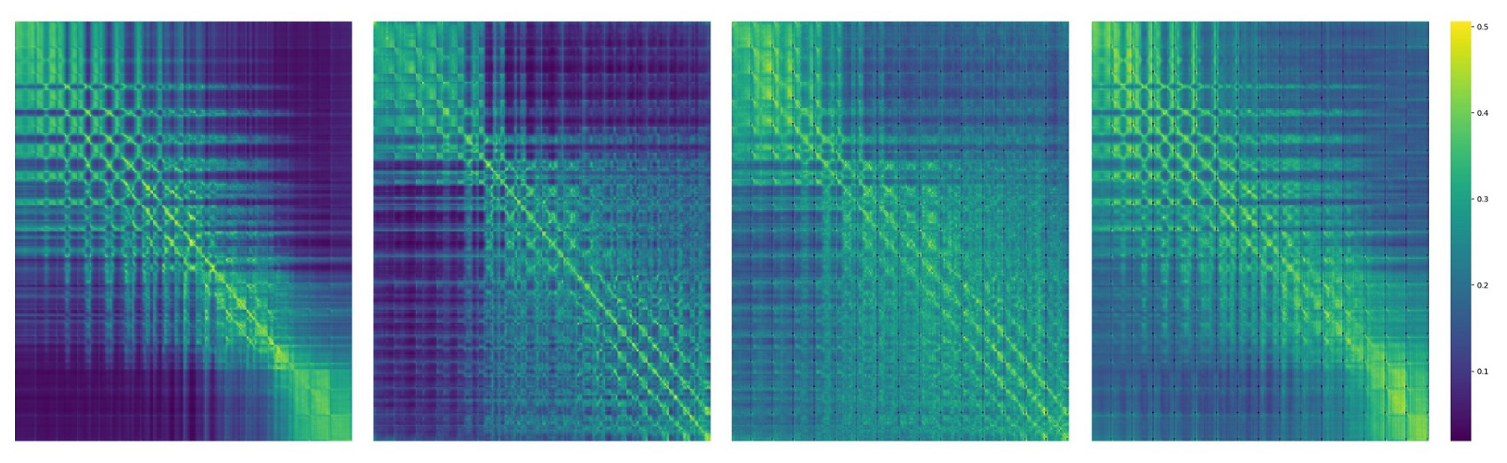
• 无法适用于下游任务：需要相互关系的下游任务无法应用

  

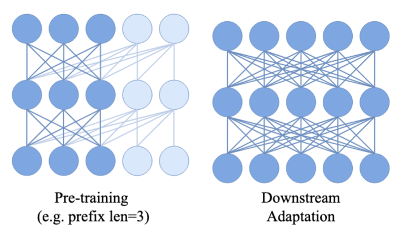
• 结构退化：图像空间结构也包含有信息

• 效率低：transformer是$\mathcal{O}\left(n^2\right)$，加上自回归就是$\mathcal{O}\left(n^6\right)$

  时间复杂度分析：

  引理：对于标准的self-attention，对于AR的复杂度为$\mathcal{O}\left(n^6\right)$，其中$h=w=n$

  证明：

  所有token的数量是$n^2$

  但值得注意的是，这是基于像素的回归，而不是基于patch的回归

  由此需要回归$n^2$次，而transformer的计算复杂度为$\mathcal{O}\left(i^2\right)$

  由此可以求得总的时间复杂度为：

  $$\sum_{i=1}^{n^2} i^2=\frac{1}{6} n^2\left(n^2+1\right)\left(2 n^2+1\right)$$

  即$\mathcal{O}\left(n^6\right)$

但需要注意：

1.此处是基于像素的回归，n代表像素数量，但在基于视觉的模型中较少使用，给出的对比方法中也是21，22年左右的方法

2.时间复杂度并不代表实际时间，只是时间随分辨率增长的趋势

基于下一尺度预测的视觉自回归

首先将一张图量化为K个多尺度的$\left(r_1, r_2, \ldots, r_K\right)$，分辨率依次递增，那么自回归就变成了：

$$p\left(r_1, r_2, \ldots, r_K\right)=\prod_{k=1}^K p\left(r_k \mid r_1, r_2, \ldots, r_{k-1}\right)$$

使用了block因果mask来保证只看到之前的token：

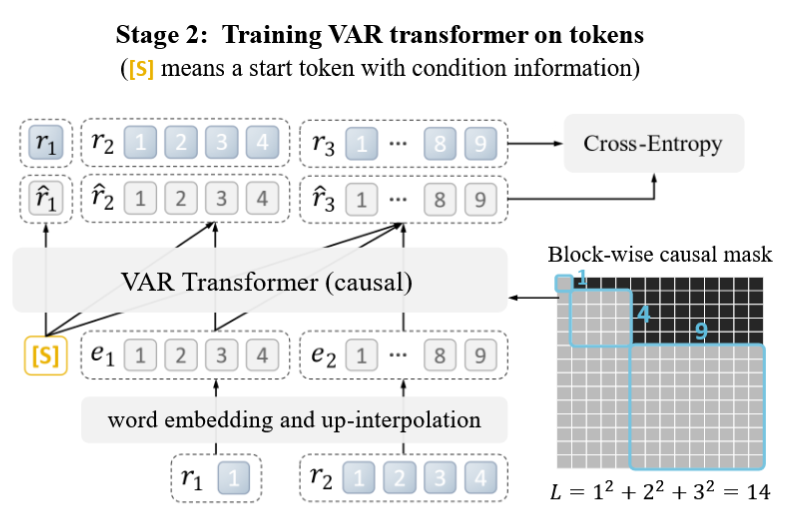
量化：采用了VQGAN中的结构，但修改了其中的多尺度量化层，使用了同样的词本：

重建的时候也用了类似VQGAN的结构：

为了解决上采样的信息损失问题，额外使用了K个卷积层

其复杂度为：$\mathcal{O}\left(n^4\right)$

假设：

• h=w=n为VQVAE获取的最大的特征图的分辨率（实际为原图分辨率）
• •生成的不同分辨率的图像的宽和高为$a^{(K-1)}=n$，其中$\alpha$为缩放系数

最终需要计算自回归的token为$\left(r_1, r_2, \ldots, r_k\right)$，一共需要计算k次，由于分辨率依次递增，每次的计算量不同：

$$\sum_{i=1}^k n_i^2=\sum_{i=1}^k a^{2 \cdot(k-1)}=\frac{a^{2 k}-1}{a^2-1}$$

最终加和得到：

$$\begin{aligned} & \sum_{k=1}^{\log _a(n)+1}\left(\frac{a^{2 k}-1}{a^2-1}\right)^2 \\ & =\frac{\left(a^4-1\right) \log n+\left(a^8 n^4-2 a^6 n^2-2 a^4\left(n^2-1\right)+2 a^2-1\right) \log a}{\left(a^2-1\right)^3\left(a^2+1\right) \log a} \\ & \sim \mathcal{O}\left(n^4\right) \end{aligned}$$

实现细节

量化器：词本所有尺度为$V=4096$，量化器在OpenImages上进行训练，下采样率为$16\times$

Transformer：

• decoder-only的transformer

• 使用adaptive normalization(AdaLN)

• 对于特定类的合成，使用了class embedding作为初始token和AdaLN的条件

• 在attention归一化query和key可以稳定训练，使用了类relu的归一化：

  $$w=64 d, \quad h=d, \quad d r=0.1 \cdot d / 24$$

  其中，$w$是宽度，$h$是head的数量，$dr$是drop比率

由此，总参数量为：

$$N(d)=\underbrace{d \cdot 4 w^2}_{\text {self-attention }}+\underbrace{d \cdot 8 w^2}_{\text {feed-forward }}+\underbrace{d \cdot 6 w^2}_{\text {adaptive layernorm }}=18 d w^2=73728 d^3$$

超参数：

$lr=10^{-4}$ per 256 batch，batch=256，AdamW(${\beta}_1=0.9, {\beta}_2=0.95, decay=0.05$)，batch=768~1024，epoch=200~350

实验

对比试验

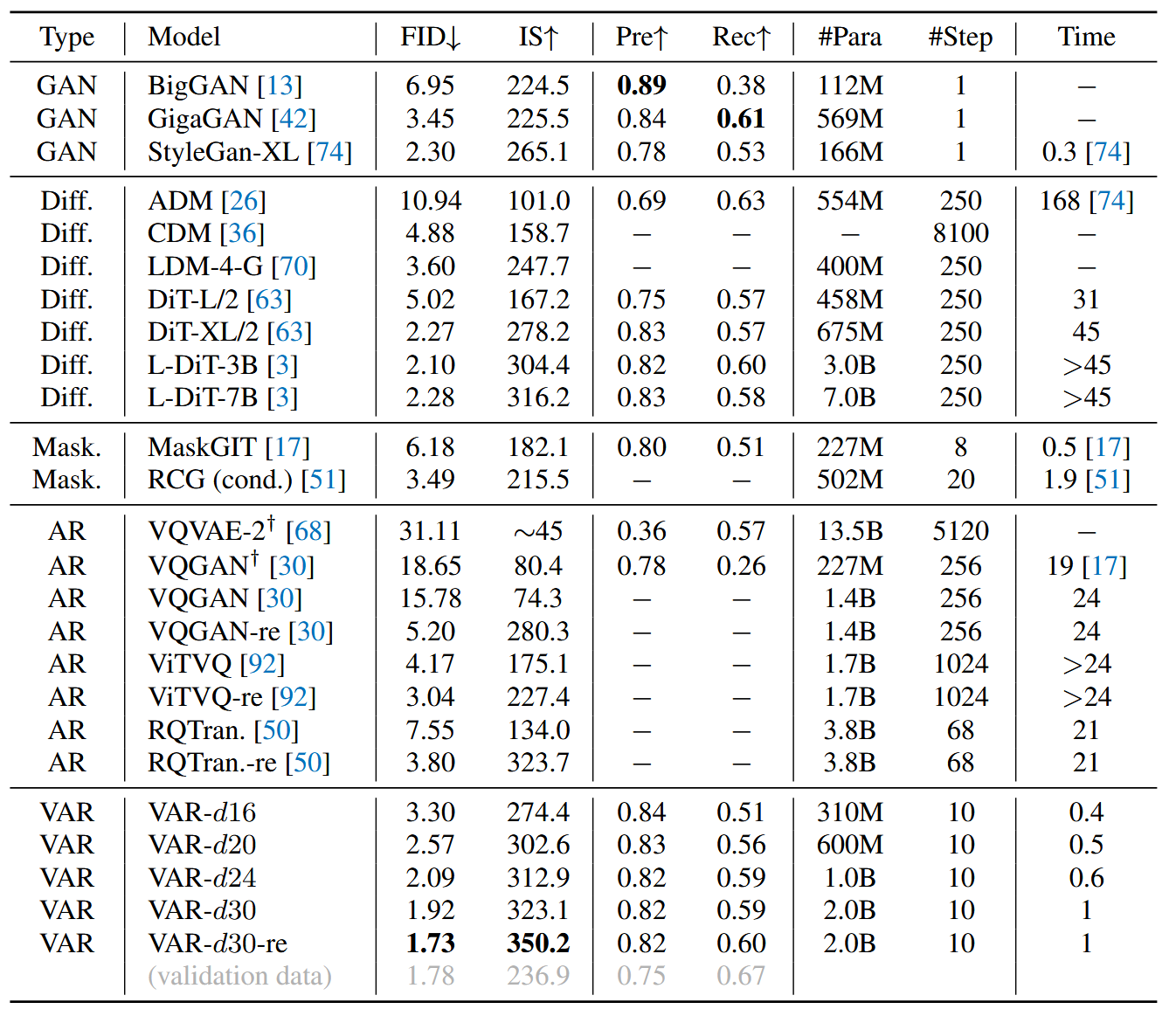
对于$256\times256$，带有类别的生成

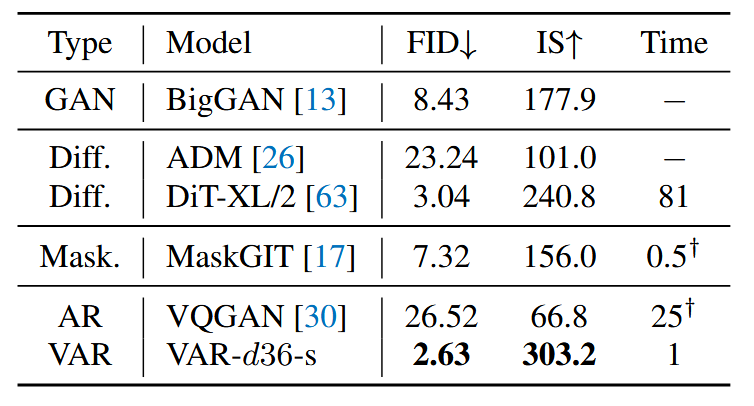
对于$512\times512$的图像：

scaling能力

之前的研究认为扩展AR模型会导致测试损失有一个可预期的下降：

$$L=(\beta \cdot X)^\alpha$$

其中，$X$可以任意为参数量$N$，训练token $T$，优化训练计算量$C_{min}$，指数上标$\alpha$表明power-law的平滑性，$L$代表被不可削减的损失$L_{\infty}$归一化的可削减损失

$$\log (L)=\alpha \log (X)+\alpha \log \beta$$

测试了$18M$到$2B$的模型，包含1.28M图像或者870B的token

总结

方法优势：

• 利用自回归的尺度预测方式，可以把多尺度特征的优势引入图像生成，自监督预训练和下游任务

• 多尺度的自回归预测，在一定程度上解决了图像自回归训练的因果依赖问题，实现了合理的视觉自回归

可能的劣势：

• 时间复杂度的计算问题：基本单位和结构设计并不一致，放在一起比较并没有实际意义，实际上，其训练速度很慢

• 对于多尺度的特征生成的方式还可能进行改进，一方面VQGAN的各层特征并不一定具有物理意义，另一方面，不同分辨率的特征纬度是不统一的