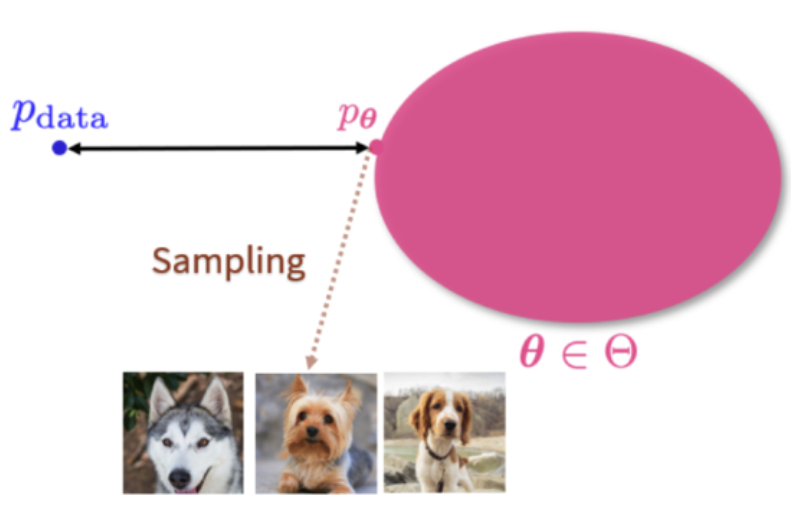
生成式模型本质上是一组概率分布。也就是说对于一个数据集，可以假设其都是从某个概率分布pdatap_{data}中独立同分布取出的随机样本，如下图所示。

My image

生成模型学习一个概率分布pθp_\theta，在推理时，在pθp_\theta上进行采样，就可以不断获取新数据。

但是，pdatap_{data}未知，形式复杂，图像维度高，数据集的样本也有限，与自然分布存在偏差，例如下图，假设模型可以学到的参数空间为Θ\Theta，进行训练后，只能得到距离数据分布pdatap_{data}最近的pθp_{\theta}，在此分布上采样获取新图像：

My image

主流的生成流派有：

  • 生成对抗网络（GAN）：通过判别器和生成器相互博弈
  • 变分自编码器（VAE）：通过一个编码器将输入图像编码为特征向量，学习高斯分布的均值和方差，解码器将特征向量转换为图像
  • 标准化流模型（NF）：从简单分布开始，通过一系列可你的转换函数转换为目标分布
  • 扩散模型：正向加噪+反向去噪
  • 自回归模型：next-token预测

GAN由于训练不稳定，基本上很少用；
VAE（例如VQVAE）等不仅用在生成模型，频繁用在其它网络中（例如很多用于生成的自回归模型会用）；
NF由于计算复杂，很少在实际中使用，但Flow matching受到其和扩散模型启发
扩散自不用多说，现阶段主流的生成形式
自回归由于训练比GAN稳定，比扩散简单，和transformer统一，也是一种新兴的方式，通常会利用VAE离散化

扩散原理

核心思想特别简单：先把清晰的目标慢慢 “模糊”（扩散过程），再学怎么把模糊的结果一步步 “还原”（逆扩散过程）。

符号定义：
x0x_0：原始数据（清晰图像）
xtx_t：第tt步扩散的带噪数据(t=0是原始数据)
T：扩散总步数
βt\beta_t：第tt步的噪声强度，随时间变化，变化情况称为差异时间表，通常从1e-4逐步增加至2e-2
αt\alpha_t：1−βt1-\beta_t，第tt 步的保留系数
αt‾\overline{\alpha_t}：aˉt=∏s=1tαt\bar{a}_t= \prod_{s=1}^t \alpha_t，累积保留系数

前向扩散

首先引入了一个马尔可夫链的加噪过程：

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right) \quad q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)=\prod_{t=1}^T q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)

前向扩散每一步对于数据加入噪声：

xt=αt⋅xt−1+1−αt⋅ϵtx_t=\sqrt{\alpha_t} \cdot x_{t-1}+\sqrt{1-\alpha_t} \cdot \epsilon_t

其中，ϵt∼N(0,I)\epsilon_t \sim \mathcal{N}(0, I)为第tt步加入的高斯噪声

对于βt\beta_t，原文中使用的是线性策略，但在OpenAI的Improved diffusion 中改进到了cosine策略（注意是根据xtx_t和x0x_0关系的公式想要αtˉ\bar{\alpha_t}按照cos的形式），通过计算：

αˉ(t)=cos⁡2(t+s1+s⋅π2)cos⁡2(s1+s⋅π2)\bar\alpha(t) = \frac{\cos^2\left(\frac{t+s}{1+s}\cdot \frac{\pi}{2}\right)} {\cos^2\left(\frac{s}{1+s}\cdot \frac{\pi}{2}\right)}

一般s=0.008s=0.008，这个公式的好处在于αtˉ(0)=1\bar{\alpha_t}(0)=1，逐渐接近于0，并且是类cos的形状(cos2cos^2)

重参数 ：由于采样的操作不可导，无法反传梯度，实际实现的时候，要用重参数（随机采样->确定函数+独立随机噪声）使得其可微，转换前的xtx_t为：

xt=N(xt;αˉtx0,(1−αˉt)I)\boldsymbol{x}_t=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)

重参数：1）x∼N(μ,σ2)x \sim N\left(\mu, \sigma^2\right)，2）x=μ+σ⋅ε,ε∼N(0,1)x=\mu+\sigma \cdot \varepsilon, \varepsilon \sim N(0,1)两者等价，但后者可微

累加性：由于是加法，可以一步计算tt时刻的噪声图像，不用多步扩散：

xt=αˉt⋅x0+1−αˉt⋅ϵx_t=\sqrt{\bar{\alpha}_t} \cdot x_0+\sqrt{1-\bar{\alpha}_t} \cdot \epsilon

证明：
由于

xt=αt⋅xt−1+1−αt⋅ϵx_t=\sqrt{\alpha_t} \cdot x_{t-1}+\sqrt{1-\alpha_t} \cdot \epsilon

那么，

xt=αt(αt−1⋅xt−2+1−αt−1⋅ϵ)+1−αt⋅ϵ=αtαt−1⋅xt−2+αt1−αt−1⋅ϵ+1−αt⋅ϵ\begin{aligned} x_t &= \sqrt{\alpha_t}\Big(\sqrt{\alpha_{t-1}} \cdot x_{t-2} + \sqrt{1-\alpha_{t-1}} \cdot \epsilon) + \sqrt{1-\alpha_t} \cdot \epsilon \\ &= \sqrt{\alpha_t}\sqrt{\alpha_{t-1}} \cdot x_{t-2} + \sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}} \cdot \epsilon + \sqrt{1-\alpha_t} \cdot \epsilon \end{aligned}

后一项的括号中本质上是两个正态分布的相加，由叠加性可以得到：

X1∼αt1−αt−1ϵ=N(0,αt(1−αt−1))X2∼1−αtϵ=N(0,1−αt)X1+X2=N(0,1−αtαt−1)\begin{gathered} X_1 \sim \sqrt{\alpha_t} \sqrt{1-\alpha_{t-1}} \epsilon=N\left(0, \alpha_t\left(1-\alpha_{t-1}\right)\right) \\ X_2 \sim \sqrt{1-\alpha_t} \epsilon=N\left(0,1-\alpha_t\right) \\ X_1+X_2=N\left(0,1-\alpha_t \alpha_{t-1}\right) \end{gathered}

那么，上式就为：

xt=αtαt−1xt−2+(1−αtαt−1)ϵx_t=\sqrt{\alpha_t \alpha_{t-1}} x_{t-2}+\left(\sqrt{1-\alpha_t \alpha_{t-1}}\right) \epsilon

后面的就可以用归纳法推导，由此q(xt∣x0)q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)仍是一个高斯分布

后向去噪

前向过程是高斯分布，后向过程也是高斯分布，后向过程可以表示为（即xtx_t已知，只需要学条件概率）：

pθ(xt−1∣xt)=N(μθ(xt,t),σt2I)p_\theta\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)=\mathcal{N}\left(\mu_\theta\left(x_t, t\right), \sigma_t^2 I\right)

其中，θ\theta可以表示为神经网络的参数

对于其中的均值和方差：

方差：通过数学推导，方差可以直接取σt2=βt\sigma_t^2=\beta_t（或者更精确的σt2=1−αˉt−11−αˉt⋅βt\sigma_t^2=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t），只需要学习均值
均值：均值可以转化为：

μθ(xt,t)=αt(1−αˉt−1)1−αˉt⋅xt+αˉt−1⋅βt1−αˉt⋅x^0(xt,t)\mu_\theta\left(x_t, t\right)=\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \cdot x_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \cdot \beta_t}{1-\bar{\alpha}_t} \cdot \hat{x}_0\left(x_t, t\right)

其中，x^0(xt,t)\hat{x}_0\left(x_t, t\right)是模型预测的原始x0x_0值，由此，均值只和x^0\hat{x}_0有关（xtx_t已知），那么模型的学习就是从已有的信息和时间tt中预测原始图片的预测项x^0\hat{x}_0

代入

x0=1αˉt(xt−1−αˉtϵt)x_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(x_t-\sqrt{1-\bar{\alpha}_t} \epsilon_t\right)

那么，均值就可以写为：

μ~t=1αt(xt−1−αt1−αˉtεt)\tilde{\mu}_t=\frac{1}{\sqrt{\alpha_t}}\left(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \varepsilon_t\right)

那么均值只和超参数αt\alpha_t，αˉt\bar{\alpha}_t，xtx_t，εt\varepsilon_t有关

目标函数

后向去噪过程可以知道，目标可以转换为xtx_t的分布->xtx_t条件下xt−1x_{t-1}的概率->均值->εt\varepsilon_t，转换为高斯噪声的分布

利用贝叶斯定理和琴生不等式，采用最大化证据下界的方法可以推导，写为：

Lsimple =Et,x0,ϵ∥ϵt−ϵ^θ(αˉtx0+1−αˉtϵ,t)∥2\mathcal{L}_{\text {simple }}=\mathbb{E}_{t, \boldsymbol{x}_0, \epsilon}\left\|\boldsymbol{\epsilon}_t-\hat{\boldsymbol{\epsilon}}_\theta\left(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2

其中，ϵ^θ(xt,t)\hat{\boldsymbol{\epsilon}}_\theta\left(\boldsymbol{x}_t, t\right)就是一个神经网络，预测噪声

条件生成

可以随机采集一个条件噪声，然后逐步去噪（也还是重参数化）：

xt−1=1αt(xt−1−αt1−αˉtϵ(xt,t))+σtz\boldsymbol{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon\left(\boldsymbol{x}_t, t\right)\right)+\sigma_t \boldsymbol{z}

使用U-Net的DDPM

结构

DDPM最初选择的是U-Net来预测噪声，包含编码器，解码器和残差链接。
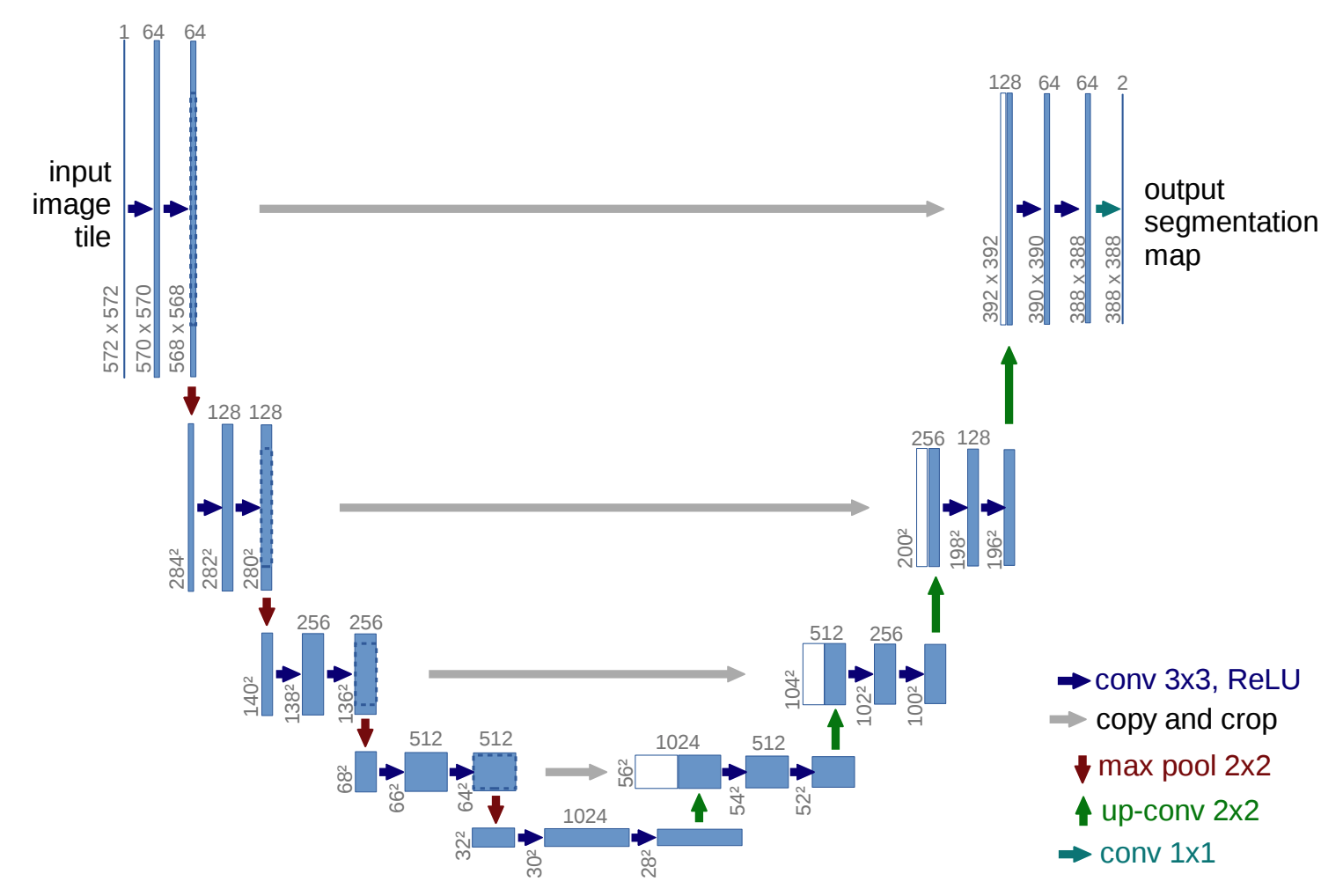
My image

宽残差卷积：DDPM中也对卷积做出了改进，使用宽残差网络作为核心结构

一般有两种残差结构，Unet的DDPM使用后一种：

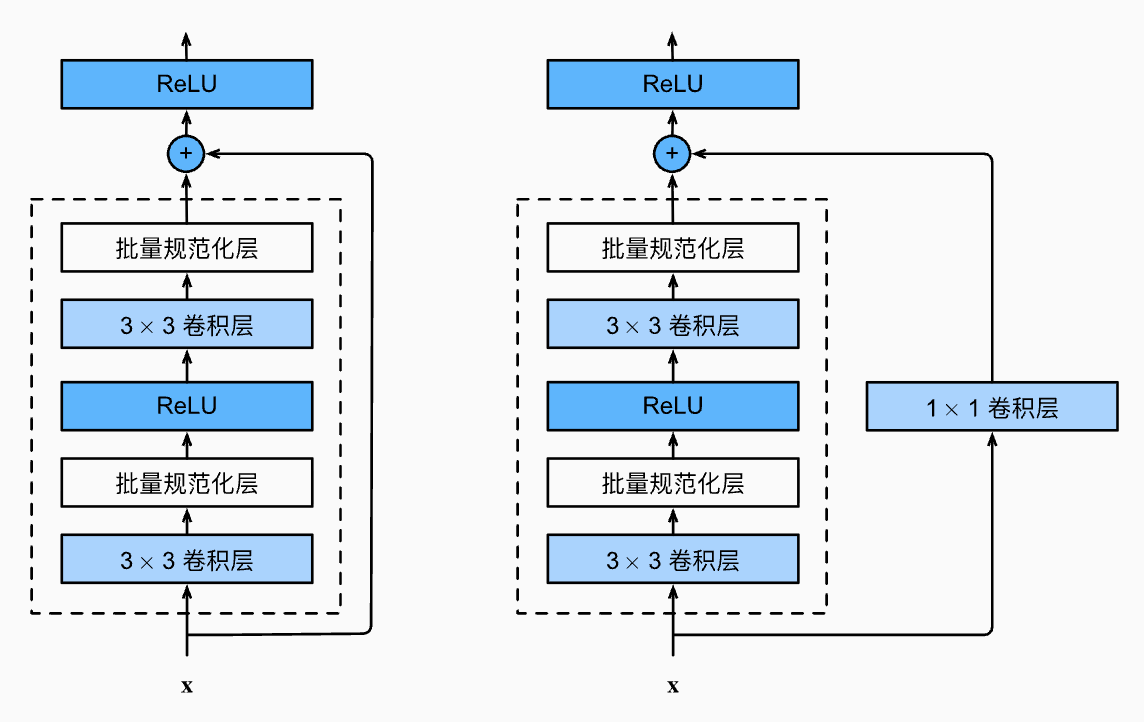
My image

宽残差网络（WRN）：
增加一个宽度因子，通道数变为原始通道数×\times宽度因子，具有更浅的宽度，并在卷积层中间加入dropout
优势：训练快，更容易并行，过拟合风险更小

注意在基于Unet的DDPM的实现中，一般会尽量使用残差链接（每个block都有残差链接），而非传统UNet中每个分辨率做残差链接

使用ConvNext也能获得更好的性能提升

时间编码：为了区分不同的时间片，加入正弦位置嵌入

注意力引入：通常在低分辨率的卷积层之间，会加入注意力层

组归一化

classifier-free引导生成：让同一个去噪网络同时学会“有条件”和“无条件”的去噪，然后在生成时把两者做线性外推来加强条件信号

缺点

DDPM通过直接在图像像素空间中进行操作实现了图像生成任务，但由于链式特性，训练和推理都很消耗资源

DDIM(Denoising Diffusion Implicit Models)

只需要对于采样器进行修改(逐步的马尔可夫过程->可重参数化，任意时间离散的非马尔可夫过程)，实现间隔多步采样

原理

在反向去噪的过程中，DDPM定义为一个马尔可夫链：

pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt)p_\theta\left(\mathbf{x}_{0: T}\right)=p\left(\mathbf{x}_T\right) \prod_{t=1}^T p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)

同时发现后验分布可以表示为一个高斯分布：

q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI)q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\mu}_t\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right)

这里，后验概率q(xt−1∣xt,x0)q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)实际上是由q(xt∣xt−1)q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)和马尔可夫性经过贝叶斯公式推导出来的

而其目标为：

Lsimple =Et,x0,ϵ∥ϵt−ϵ^θ(αˉtx0+1−αˉtϵ,t)∥2\mathcal{L}_{\text {simple }}=\mathbb{E}_{t, \boldsymbol{x}_0, \epsilon}\left\|\boldsymbol{\epsilon}_t-\hat{\boldsymbol{\epsilon}}_\theta\left(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2

但我们从损失出发可以发现，优化目标只依赖于边缘分布q(xt∣x0)q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)(只包含单个时间步，不包含中间路径)，而非整个联合分布q(x1:T∣x0)q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)(包含整个扩散的路径的概率)，由此可以直接定义q(xt−1∣xt,x0)q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)解除马尔可夫约束

也就是说，只需要q(xt−1∣xt)q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)已知，而且是高斯分布的形式，就可以用DDPM的目标函数来训练模型

由此，DDIM将前向过程的联合分布重新定义为：

qσ(x1:T∣x0)=qσ(xT∣x0)∏t=2Tqσ(xt−1∣xt,x0)q_\sigma\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)=q_\sigma\left(\mathbf{x}_T \mid \mathbf{x}_0\right) \prod_{t=2}^T q_\sigma\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0\right)

其中，σ\sigma为一个实数超参数，对于t=0t=0，qσ(xT∣x0)=N(αTx0,(1−αT)I)q_\sigma\left(\mathbf{x}_T \mid \mathbf{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_T} \boldsymbol{x}_0,\left(1-\alpha_T\right) \boldsymbol{I}\right)与DDPM中的相同，仍为高斯分布，对t>1t>1，定义：

qσ(xt−1∣xt,x0)=N(αt−1x0+1−αt−1−σt2⋅xt−αtx01−αt,σt2I)q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{t-1}} \boldsymbol{x}_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2} \cdot \frac{\boldsymbol{x}_t-\sqrt{\alpha_t} \boldsymbol{x}_0}{\sqrt{1-\alpha_t}}, \sigma_t^2 \boldsymbol{I}\right)

由此，对于任意时刻，qσ(xt∣x0)=N(αtx0,(1−αt)I)q_\sigma\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0,\left(1-\alpha_t\right) \boldsymbol{I}\right)都满足(为高斯分布)

respacing

基于DDIM，就可以采用respacing进行加速(性能损耗较小)

可以在[1, …, T]的范围(训练时)，可以采样一个子集{xτ1,…,xτS}\left\{\boldsymbol{x}_{\tau_1}, \ldots, \boldsymbol{x}_{\tau_S}\right\}来进行生成